1．设集合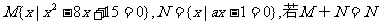，则实数a的组成的集合Q是　　　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．{3，5}　　　　　　　　 B．{0，3，5}　　　　　 C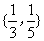．　　　　　　　 D．

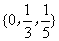
22．(本题满分14分)

　　 定义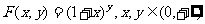

　 (1)令函数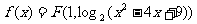的图象为曲线c₁，曲线c₁与y轴交于点A(0，m)，过坐标原点O作曲线c₁的切线，切点为B(n，t)(n＞0)设曲线c₁ 在点A、B之间的曲线段与OA、OB所围成图形的面积为S，求S的值；

　 (2)当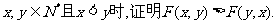

21．(本题满分12分)

　　　　 定义：两个连续函数(图象不间断)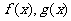在区间[a，b]上都有意义，我们称函数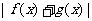在[a，b]上的最大值叫做函数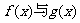在区间[a，b]上的“绝对和”。

　 (1)试求函数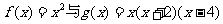在闭区间[-2，2]上的“绝对和”；

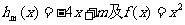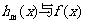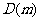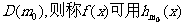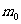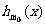　 (2)设都是定义在闭区间[1，3]上，记的“绝对和”为D_m，如果的最小值是“替代”，试求的值，使可用“替代”。

20．(本题满分12分)

　　　　 诺贝尔奖发放方式为：每年一闪，把奖金总额平均分成6份，奖励在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出最有益贡献的人，每年发放奖金的总金额是基金在该年度所获利息的一半，另一半利息用于基金总额，以便保证奖金数逐年增加。假设基金平均年利率为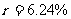。资料显示：1999年诺贝尔奖发放后基金总额约为19800万美元。设表示为第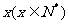年诺贝尔奖发放后的基金总额(1999年记为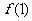，2000年记为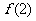，……，依次类推)

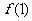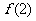　 (1)用表示与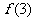，并根据所求结果归纳出函数的表达式；

　 (2)试根据的表达式判断网上一则新闻“2009年度诺贝尔奖各项奖金高达150万美元”是否为真，并说明理由。

(参考数据：)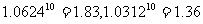

19．(本题满分12分)

已知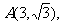O是原点，点

　 　(1)求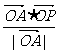的最大值；

　 (2)求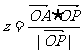的取值范围。

18．(本题满分12分)

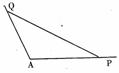
　　 如图所示，角A为钝角，且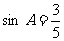，点P、Q分别在角A的两边上。

　 (1)AP=5，PQ=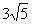，求AQ的长；

　 (2)设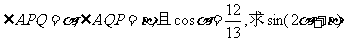的值。

17．(本题满分12分)

　　 解关于x的不等式：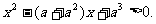

16．函数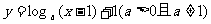的图象恒过定点A，若点A在一次函数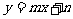的图象上，其中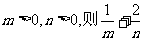的最小值为　　　　　 。

15．已知　　　　 。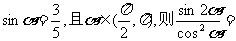

14．不等式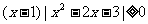的解集为　　　　　　 。