20．(本小题满分13分)

　　 某种细菌m小时分裂一次(每一次分裂成两个，分裂所需的时间忽略不计)研究开始时仅有一个细菌，在研究过程中不断进行分裂，则细菌总数y是时间t的函数，记作

　 (I)当m=1时，在所给坐标系中画出的图象；

　 (II)当m=1时，研究进行到第n小时时细菌的总数为a_n，若关于n的式子表示a_n，并探究是否存在实数列，使得　　　　 对一切正整数n都成立？若存在，请求出数列的通项公式；若不存在，请说明理由。

19．(本小题满分12分)

　 将圆向左平移1个单位，再向上移2个单位，得到圆O，直线与圆O相交于A，B两点，若圆O上存在点C，使，求直线的方程及对应的点C的坐标。

18．(本小题满分12分)

　　 已知数列为负整数。

　 (I)用a，b表示

　 (II)若的通项

17．(本小题满分12分)

　 　若函数的图象与直线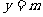相切，并且切点的横坐标依次构成公差为的等差数列。

　 (I)求实数m的值；

　 (II)求函数的单调递增区间；

16．(本小题满分12分)

已知之间满足关系

　 (I)用k表示

　 (II)求的取值范围。

15．已知满足，切其外接圆直径为，又点M、N满足=　　　　　 .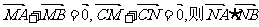

14．直线的最小值为　　　 。

13．过点A(2，-2)作曲线的切线，则切线方程为　　　　　　　　 。

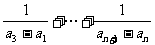12．在数列中， 等于　　　　　　 。

11．已知的解A，B，C所对的边分别为a，b，c，若 的取值范围是　　　　　　　　　　　 。