
4、已知集合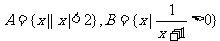 ,则
,则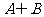 =____________。
=____________。
3、计算: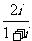 =_______________(
=_______________(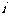 为虚数单位)。
为虚数单位)。
2、已知函数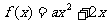 是奇函数,则实数a=______________。
是奇函数,则实数a=______________。
1、函数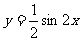 的最小正周期T=_________________________。
的最小正周期T=_________________________。
22.(本小题满分14分)
已知数列 的相邻两项
的相邻两项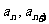 是关于x的方程
是关于x的方程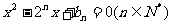 的两根,且a1=1。
的两根,且a1=1。
(1)求证:数列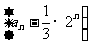 是等比数列;
是等比数列;
(2)设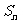 是数列
是数列 的前
的前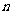 项和, 问是否存在常数
项和, 问是否存在常数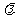 ,使得
,使得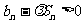 对任意
对任意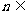 N
N 都成立,若存在, 求出
都成立,若存在, 求出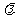 的取值范围; 若不存在, 请说明理由.
的取值范围; 若不存在, 请说明理由.
21.(本小题满分12分)
设aÎR,f (x)为奇函数,且f (2x)=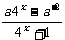 .
.
(1)求a的值及f(x)的解析式和值域;
(2)g(x)=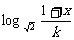 ,若xÎ
,若xÎ 时,
时, ≤g(x)恒成立,求实数k的取值范围。
≤g(x)恒成立,求实数k的取值范围。
20.(本小题满分12分)
已知点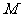 在椭圆
在椭圆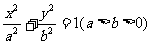 上, 以
上, 以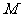 为圆心的圆与
为圆心的圆与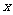 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点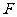 .
.
(1)若圆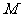 与
与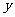 轴相切,求椭圆的离心率;
轴相切,求椭圆的离心率;
(2)若圆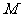 与
与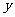 轴相交于
轴相交于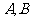 两点,且
两点,且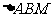 是边长为2的正三角形,求椭圆的方程.
是边长为2的正三角形,求椭圆的方程.
19.(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
18.(本小题满分12分)
圆经过点A(2,-3)和B(-2,-5).
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
17.(本小题满分12分)
已知函数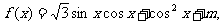 其中m为实常数。求
其中m为实常数。求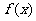 的最小正周期、单调递增区间、所有的对称轴方程、值域。
的最小正周期、单调递增区间、所有的对称轴方程、值域。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com