
5.函数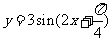 的图象
的图象
A.关于直线 对称 B.关于直线
对称 B.关于直线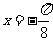 对称
对称
C.关于点 对称 D.关于点
对称 D.关于点 对称
对称
4. 中,点
中,点 、
、 、
、 分别为
分别为 、
、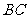 、
、 的中点,则
的中点,则
A.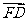 B.
B. C.
C. D.
D.
3.已知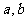 为两条不同直线,
为两条不同直线, 、
、 为两个不同平面,且
为两个不同平面,且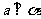 ,
, ,则假命题是
,则假命题是
A.若 ,则
,则 B.若
B.若 ,则
,则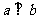
C.若 、
、 相交,则
相交,则 、
、 相交 D.若
相交 D.若 、
、 相交,则
相交,则 、
、 相交
相交
2.设 是等差数列,
是等差数列,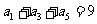 ,
,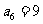 ,则其前6项和为
,则其前6项和为
A.12 B.24 C.36 D.48
1.已知集合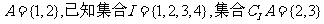 ,则集合
,则集合 =
=
A.{1,4} B.{1,2,4} C.{1,3,4} D.{1,2,3,4}
21.(本小题满分13分)已知圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切.
(1)求圆C的方程;
(2)设直线 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数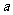 的取值范围;
的取值范围;
(3)在(Ⅱ)的条件下,是否存在实数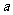 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点P(-2,4),若存在,求出实数
过点P(-2,4),若存在,求出实数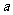 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20.(本题12分)如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1 中,已知AC =BC = AA1=a,∠ACB =90°,F是棱BB1上任意一点,D 是A1B1 中点。

(1)当F是BB1中点时,求证:A1B//面C1DF;
(2)求证:面C1DF ⊥平面A1B1BA ;
(3)请问, 当点F 在BB1 上什么位置时,会使得AB1 ⊥平面C1DF?并证明你的结论.
19.(本题10分)已知数列 中,
中, 前
前 项和为
项和为 ,且点
,且点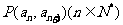 在直线
在直线 上.
上.
(1)求证: 是等差数列;
是等差数列;
(2)设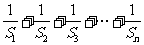 =
=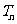 ,求证
,求证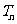 <2.
<2.
18.(本题10分)求过两直线 和
和 的交点, 且分别满足下列条件的直线l的方程.
的交点, 且分别满足下列条件的直线l的方程.
(1)直线l与直线 垂直;
垂直;
(2)坐标原点与点A(1,1)到直线l的距离相等.
17.若数列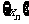 满足:
满足: 且
且 ,则它的通项
,则它的通项 等于 .
等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com