
2.△ABC中A:B:C=1:2:3则a:b: c= 。
1.△ABC中已知∠A=60°,AB :AC=8:5,面积为10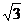 ,则其周长为
。
,则其周长为
。
3.在△ABC中,“A>30°”是“sinA>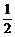 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
§36 解三角形 (2)
[典型例题讲练]
例3在△ABC中 A=45°,B:C = 4:5最大边长为10,求角B、C、外接圆半径及面积S
变式:在△ABC中以知A=30°a、b分别为角A、B对边,且a=4=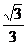 b
b
解此三角形
例4.△ABC的周长为12, 且sinA·cosB-sinB=sinC-sinA·cosC,则其面积最大值为 。
变式:△ABC三内角A、B、C成等差数列,则cos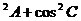 的最小值为
。
的最小值为
。
[课堂小结]
常用方法: (1)A+B+C=180° 可进行角的代换
(2)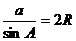 可进行边角互换
可进行边角互换
(3)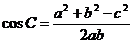 可进行角转化为边
可进行角转化为边
(4)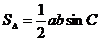 面积与边角联系。
面积与边角联系。
[课堂检测]
2.△ABC中,a、b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=30 △ABC的面积为
△ABC的面积为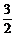 ,那么b等于
,那么b等于
A.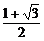 B.1+
B.1+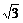 C.
C.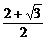 D.2+
D.2+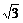
1.下列条件中,△ABC是锐角三角形的是
A.sinA+cosA=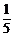 B.
B.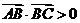
C.tanA+tanB+tanC>0 D.b=3,c=3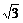 ,B=30°
,B=30°
1.
变式: 在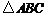 中,
中,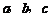 分别是三个内角
分别是三个内角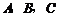 的对边.若
的对边.若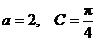 ,
,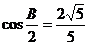 ,则
,则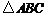 的面积
的面积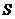 =________________
=________________
例2在ΔABC中,若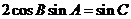 ,则ΔABC的形状为
.
,则ΔABC的形状为
.
变式1: 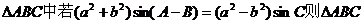 是( )
是( )
A、等腰三角形 B、直角三角形
C、等腰直角三角形 D、等腰或直角三角形。
[课堂小结]
利用正弦,余弦定理,可以解决以下几类有关三角形的问题.
[课堂检测]
4.在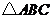 中,若
中,若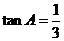 ,
,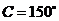 ,
,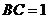 ,则
,则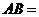
[典型例题讲练]
例1
在ΔABC中,已知a=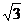 ,b=
,b=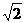 ,B=45°,求A,C及边c.
,B=45°,求A,C及边c.
3.在△ABC中,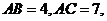
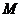 为
为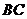 的中点,且
的中点,且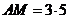 ,则
,则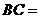 .
.
2.在△ABC中,角A、B、C所对的边分别是a、b、c,若三角形的面积S=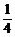 (a2+b2-c2),则∠C的度数是_______.
(a2+b2-c2),则∠C的度数是_______.
1.在△ABC中,“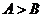 ”是“
”是“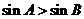 ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com