
2.化简:(+)+(+)=
1.四边形ABCD满足=,且||=||,则四边形ABCD是 .
4.已知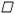 ABCD中,点E是对角线AC上靠近A的一个三等分点,设=a,=b,则向量
ABCD中,点E是对角线AC上靠近A的一个三等分点,设=a,=b,则向量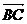 等于 ( )
等于 ( )
A. 2a+b B.2a-b C.b-2a D.-b-2a
§38 平面向量 1 (2)
[典型例题讲练]
例3如图,=a,=b,=t(t∈R),当P是(1)中点,(2)的三等分点(离A近的一个)时,分别求.
变式: 在△OAB中,C是AB边上一点,且=λ(λ>0),若=a,=b,试用a,b表示.
例4.某人在静水中游泳,速度为4千米/时,他在水流速度为4千米/时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
变式: 一艘船从A点出发以2 km/h的速度向垂直于对岸的方向行驶,同时河水的流速为2 km/h,求船实际航行速度的大小与方向(用与流速间的夹角表示).
[课堂小结]
在理解向量加减法定义的基础上,掌握向量加法的三角形法则与平行四边形法则以及减法的三角形法则,并了解向量加减法在物理学中的应用。
[课堂检测]
3.判断下列命题是否正确,若不正确,请简述理由.
①向量与是共线向量,则A、B、C、D四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形的充要条件是=;
⑤模为0是一个向量方向不确定的充要条件;
⑥共线的向量,若起点不同,则终点一定不同.
2.已知正方形ABCD边长为1,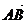 +
+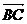 +
+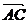 模等于( )
模等于( )
A.0 B.3 C.2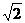 D.
D.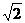
1.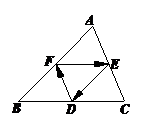 如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
(1)与向量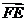 共线的有
.
共线的有
.
(2)与向量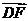 的模相等的有
.
的模相等的有
.
(3)与向量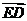 相等的有
.
相等的有
.
4. 已知C是线段AB上一点,
已知C是线段AB上一点,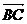 =
=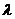
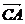 (
(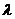 >0).若
>0).若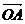 =
=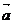 ,
,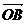 =
=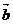 ,请用
,请用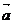 ,
,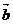 表示
表示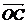 .
.
[典型例题讲练]
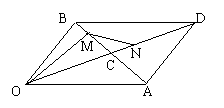
例1、如图所示,OADB是以向量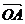 =
=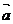 ,
,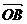 =
=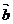 为边的平行四边形,又BM=
为边的平行四边形,又BM=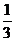 BC,CN=
BC,CN=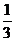 CD.试用
CD.试用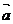 ,
,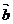 表示
表示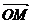 ,
,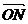 ,
,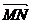 .
.
变式: 平行四边形ABCD中,M、N分别为DC、BC的中点,已知=c,=d,试用c,d表示和.
例2设两个非零向量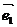 、
、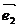 不是平行向量
不是平行向量
(1)如果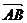 =
=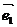 +
+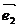 ,
,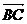 =2
=2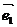 +8
+8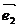 ,
,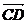 =3(
=3(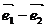 ),求证A、B、D三点共线;
),求证A、B、D三点共线;
(2)试确定实数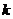 的值,使
的值,使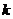
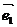 +
+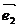 和
和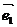 +
+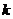
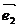 是两个平行向量.
是两个平行向量.
变式: 已知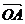 、
、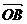 不共线,
不共线,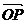 = a
= a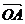 +b
+b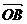 .求证:A、P、B三点共线的充要条件是a+b=1.
.求证:A、P、B三点共线的充要条件是a+b=1.
[课堂小结]
向量是既有大小又有方向的量,应用概念解题,注意数形结合;能够从图形和代数式两个角度理解向量的加减以及数乘运算。
[课堂检测]
3.设M为△ABC的重心,则下列各向量中与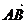 共线的是 ( )
共线的是 ( )
A.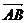 +
+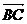 +
+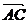 B.
B.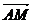 +
+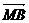 +
+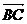
C.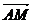 +
+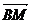 +
+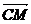 D.3
D.3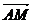 +
+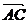
2.若ABCD为正方形,E是CD的中点,且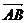 =
=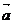 ,
,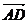 =
=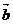 ,则
,则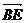 等于( )
等于( )
A.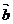 +
+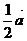 B.
B.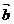
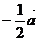 C.
C.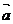 +
+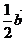 D.
D.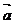
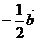
1.判断下列命题是否正确:
⑴两个向量相等的充要条件是它们的起点相同,终点相同; ( )
⑵若四边形ABCD是平行四边形,则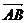 =
=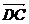 ; ( )
; ( )
⑶若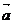 ∥
∥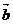 ,
,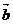 ∥
∥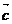 ,则
,则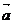 ∥
∥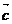 ; ( )
; ( )
⑷若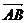 与
与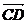 是共线向量,则A、B、C、D四点共线; ( )
是共线向量,则A、B、C、D四点共线; ( )
⑸若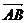 +
+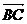 +
+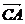 =
=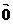 ,则A、B、C三点共线; ( )
,则A、B、C三点共线; ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com