
1.要得到函数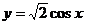 的图象,只需将函数
的图象,只需将函数 图象上的点的
图象上的点的 坐标
坐标 到原来的
到原来的 倍,再向
倍,再向 平移
平移 个单位
个单位
2.
[课堂检测]
1.
5.函数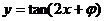 的图象过点
的图象过点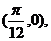 则
则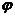 的一个值是
的一个值是
[典型例题讲练]
例1试说明下列函数的图象与函数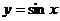 图象间的变换关系:
图象间的变换关系:
(1)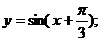 (2)
(2)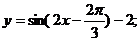 (3)
(3)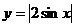
例2(1)将函数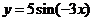 的周期扩大到原来的2倍,再将函数图象左移
的周期扩大到原来的2倍,再将函数图象左移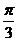 ,得到图象对应解析式是
,得到图象对应解析式是
(2)若函数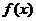 图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿
图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿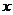 轴向右平移
轴向右平移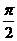 个单位,向下平移3个单位,恰好得到
个单位,向下平移3个单位,恰好得到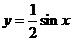 的图象,则
的图象,则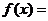 .
.
(3)先将函数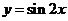 的图象向右平移
的图象向右平移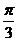 个单位长度,再将所得图象作关于
个单位长度,再将所得图象作关于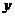 轴的对称变换,则所得函数图象对应解析式为
.
轴的对称变换,则所得函数图象对应解析式为
.
例3已知函数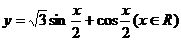 ,
,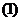 用“五点法”画出它的图象;
用“五点法”画出它的图象; 求它的振幅,周期及初相;
求它的振幅,周期及初相;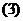 说明该函数的图象可由
说明该函数的图象可由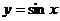 的图象经怎样的变换得到?
的图象经怎样的变换得到?
[课堂小结]
4.如果把函数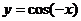 的图象向右平移2个单位后所得图象的函数解析式为
的图象向右平移2个单位后所得图象的函数解析式为
3.函数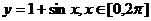 的图象与直线
的图象与直线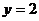 交点个数是
交点个数是 个
个
2.用“五点法”画函数 的图象时,所取五点为
的图象时,所取五点为
1.函数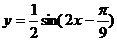 的振幅是
的振幅是 ,频率是
,频率是 ,初相是
,初相是
2. 由函数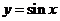 的图象到函数
的图象到函数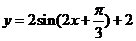 的图象的变换方法之一为:
的图象的变换方法之一为:
①将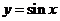 的图象向左平移
的图象向左平移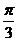 个单位得
图象,
个单位得
图象,
②再保持图象上各点纵坐标不变,横坐标变为原来的 得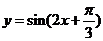 图象,
图象,
③再保持图象上各点横坐标不变,纵坐标变为原来的 倍得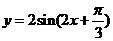 图象,
图象,
④最后将所得图象向 平移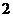 个单位得
个单位得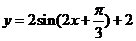 的图象.
的图象.
这种变换的顺序是:①相位变换②周期变换③振幅变换。
若将顺序改成②①③呢?
[基本训练]
1.“五点法”画正弦、余弦函数和函数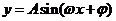 的简图,五个特殊点通常都是取三个
点,一个最 点,一个最 点;
的简图,五个特殊点通常都是取三个
点,一个最 点,一个最 点;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com