3.若函数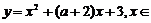[a，b]的图象关于直线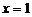对称，则.

2.求二次函数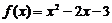在下列区间的最值

①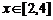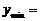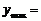，______，______；.②，______，______；

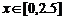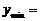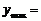③，_______，______.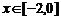

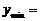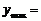1.二次函数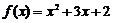的顶点式为________；对称轴为________ 最小值是______.

4.对于区间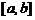上连续不断且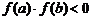的函数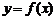，通过不断地把函数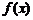的零点所在的区间__________，使区间的两端点逐步逼近__________，进而得到零点近似值的方法叫做__________.

[基本训练]

3.一般地，一元二次方程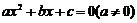的__________就是函数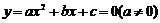的值为0时的自变量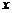的值，也就是_______________.因此，一元二次方程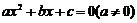的根也称为函数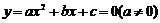的________.二次函数的解析式有三种常用表达式:(1)一般式_________________________；(2)顶点式_________________________；(3)零点式______________________________.

2.幂函数的性质：(1)所有幂函数在_______________都有定义，并且图象都过点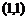，因为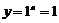，所以在第________象限无图象；(2)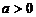时，幂函数的图象通过___________，并且在区间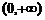上__________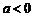，时，幂函数在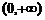上是减函数，图象___________原点，在第一象限内以___________作为渐近线.

1.形如________________的函数叫做幂函数，其中________是自变量，________是常数，如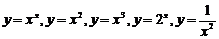，其中是幂函数的有___________　　　　 ____.

3.了解二次函数的零点与相应的一元二次方程的根的联系.

[基础知识]

2.熟悉二次函数解析式的三种形式，掌握二次函数的图形和性质.

1.了解幂函数的概念，结合函数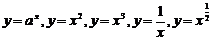的图象，了解它们的单调性和奇偶性.