
3.集合A={y|y=-x2+4,x∈N,y∈N}的真子集的个数为 ( )
A. 9 B.8 C. 7 D. 6
2.已知方程x2-px+15=0与x2-5x+q=0的解集分别为A与B,A∩B={3},则p+q的值是 ( )
A. 14 B.11 C.7 D. 2
1. 设M={0,1,2,4,5,7},N={1,4,6,8,9},P={4,7,9},则(M∩N)∪(M∩P)等于 ( )
A. {1,4} B. {1,7} C. {4,7} D. {1,4,7}
2. 已知A={x|-x2+3x+10≥0},
B={x|m≤x≤2 m -1},若B A,
A,
求实数m的取值范围.
[解]
实数m的取值范围:(- , 3) .
, 3) .
例3: 已知集合A={x|x2+4ax-4a+3=0},
B={x|x2+(a-1)x+a2=0},C={x|x2+2ax-2a=0},
其中至少有一个集合不是空集,求实数a
的取值范围.
分析:
此题若从正面入手,要对七种可能情况逐
一进行讨论,相当繁琐;若考虑其反面,则
只有一种情况,即三个集合全是空集.
[解]
当三个集合全是空集时,所以对应的三个
方程都没有实数解,
即

解此不等式组,得
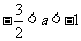
∴所求实数a的取值范围为:
a≤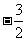 ,或a≥-1.
,或a≥-1.
点评:
采用“正难则反”的解题策略,具体地说,
就是将所研究的对象的全体视为全集,求
出使问题反面成立的集合,那么这个集合
的补集便为所求.
[师生互动]
|
学生质疑 |
|
|
教师释疑 |
|
1. 设A={x|x2-x-2<0},B={x||x|=y+1,y∈A},
求:
 ,A∪B,A∩
,A∪B,A∩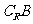 ,
,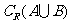
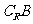 ∩
∩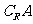
[解]
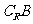 =(-
=(- ,-3]∪[3,+
,-3]∪[3,+ )∪{0};
)∪{0};
A∪B=(-3,3);
A∩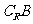 ={0};
={0};
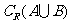 =(-
=(- ,-3]∪[3,+
,-3]∪[3,+ ).
).
2.某校有A、B两项课外科技制作小组,50名学生中报名参加A组的人数是全体学生人数的3/5,报名参加B组的人数比报名参加A组的人数多3人,两组都没有报名的人数是同时报名的人数的1/3还多1人,求同时报名参加A、B两组人数及两组都没有报名的人数.
[解]
同时报名参加A、B组的人数为21人,
两组都没有报名的人数为8人.
例2:已知全集U=R,集合A={x|x2-x-6<0},
B={x|x2+2x-8>0},C={x|x2-4ax+3a2<0},
(1)试求a的取值范围,使A∩B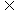 C;
C;
(2)试求a的取值范围,使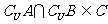
分析:
U=R,A=(-2,3),B=(- ,-4)∪(2,+
,-4)∪(2,+ ),故A∩B=(2,3),
),故A∩B=(2,3),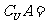
(- ,-2]∪[3,+
,-2]∪[3,+ ),
),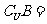 [-4,2],
[-4,2],
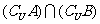 =[-4,-2],
=[-4,-2],
x2-4ax+3a2<0即(x-3a)(x-a)<0,
 ∴当a<0时,C=(3a,a),
∴当a<0时,C=(3a,a),
当a=0时,C=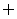 ,
,
当a>0时,C=(a,3a),
(1)
要使A∩B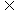 C,集合数轴知,
C,集合数轴知,
 解得 1≤a≤2;
解得 1≤a≤2;
(2)
类似地,要使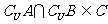 必有
必有
 解得
解得 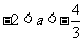
[解]
解答过程只需要将上面的分析整理一下
即可.
点评:
①研究不等式的解集的包含关系或进行集
合的运算时,充分利用数轴的直观性,便
于分析与转化.
②注意分类讨论的思想在解题中的运用,在
分类时要满足不重复、不遗漏的原则.
追踪训练二
1. 设U={x|0<x<10,x∈N+},若A∩B={3},
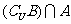 ={1,5,7},
={1,5,7},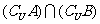
={9},求集合A,B.
[解]
A={1,3,5,7},
B={2,3,4,6,8}.
4.集合问题多与函数、方程有关,要注意
各类知识的融会贯通.
[精典范例]
例1. 设U={1,2,3,4,5},且A∩B={2},
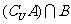 ={4},
={4},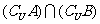
={1,5},则下列结论正确的是
( )
A.3∈A,3∈B
B.2∈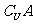 ,3∈B
,3∈B
 C.3∈
C.3∈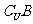 ,3∈A
,3∈A
D.3∈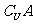 ,3∈
,3∈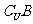
分析:按题意画出Venn图即可找出选择
的分支.
[解]
画出满题意足Venn图:
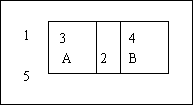
由图可知:3∈A且3 B,即3∈A且
B,即3∈A且
3∈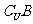 , ∴ 选C.
, ∴ 选C.
点评:
本题可用排除法来解,若选A,则3∈
A∩B,与已知A∩B={2}矛盾,……显然这种方法没有Venn图形象直观,这也突出数形集结合的思想在集合中的运用.
追踪训练一
3.含参数的集合问题,多根据集合的的互异性处理,有时需要用到分类讨论、数形集结合的思想.
2.关于集合中的运算,一般应把各参与运算的集合化到最简形式,然后再进行运算.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com