
20.05,20.15,…,59.95.
因此,各圈的周长分别为
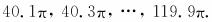
因为各圈半径组成首项为20.05,公差为0.1的等差数列,设圈数为n,则
8. 如果两等差数列有公共项,那么由它们的公共项顺次组成的新数列也是等差数列,且新等差数列的公差是原两等差数列公差的最小公倍数.
如果两等差数列有公共项,那么由它们的公共项顺次组成的新数列也是等差数列,且新等差数列的公差是原两等差数列公差的最小公倍数.
注意:公共项仅是公共的项,其项数不一定相同,即研究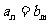 .
.
[精典范例]
[例1]某剧场有20排座位,后一排比前一排多2个座位,最后一排有60个座位,这个剧场共有多少个座位?
[解] 这个剧场各排的座位数组成等差数列,其中公差d=2,项数n=20,且第20项是a20=60?
由等差数列的通项公式,得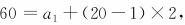
所以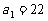
由等差数列的求和公式,得
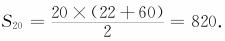
答 这个剧场共有820个座位.
[例2]某种卷筒卫生纸绕在盘上,空盘时盘芯直径40mm,满盘时直径120mm已知卫生纸的厚度为0.1mm,问:满盘时卫生纸的总长度大约是多少米(精确到1m)?

[解]卫生纸的厚度为0.1mm,可以把绕在盘上的卫生纸近似地看做是一组同心圆,然后分别计算各圆的周长,再求总和.由内向外各圈的半径分别为
7.若等差数列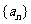 、
、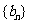 的前
的前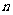 和分别为
和分别为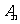 、
、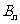 ,且
,且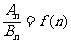 ,则
,则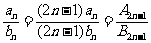
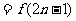 .
.
6.在等差数列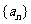 中,当项数为偶数
中,当项数为偶数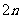 时,
时,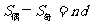 ;项数为奇数
;项数为奇数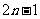 时,
时,
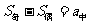 ,
,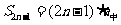
(这里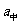 即
即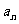 );
);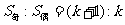 。
。
5.若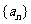 、是等差数列,
、是等差数列,
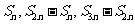 ,…也成等差数列
,…也成等差数列
4.在等差数列中,每隔相同的项抽出来的项按照原来顺序排列,构成的新数列是等差数列.
3.当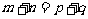 时,则有
时,则有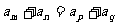 ,
,
特别地,当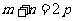 时,则有
时,则有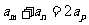
2.若公差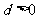 ,则为递增等差数列,若公差
,则为递增等差数列,若公差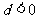 ,则为递减等差数列,若公差
,则为递减等差数列,若公差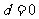 ,则为常数列。
,则为常数列。
1.当公差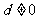 时,等差数列的通项公式
时,等差数列的通项公式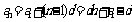 是关于
是关于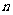 的一次函数,且斜率为公差
的一次函数,且斜率为公差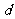 ;前
;前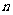 和
和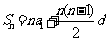
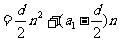 是关于
是关于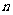 的常数项为0的二次函数.
的常数项为0的二次函数.
3.利用等差数列解决相关的实际问题。
[自学评价]
等差数列的性质:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com