
3. 两等差数列{an}、{bn}的前n项和的比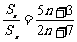 ,则
,则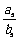 的值是( B )
的值是( B )
A.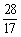 B.
B.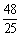 C.
C.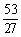 D.
D.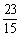
2.等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项的和为( C )
A.130 B.170 C.210 D.260
1. 已知在等差数列{an}中,a1<0,S25=S45,若Sn最小,则n为( B )
A.25 B.35 C.36 D.45
3.对等差数列前项和的最值问题有两种方法:
(1)利用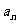 :当
:当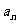 >0,d<0,前n项和有最大值
>0,d<0,前n项和有最大值 可由
可由
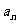 ≥0,且
≥0,且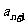 ≤0,求得n的值
≤0,求得n的值
当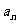 <0,d>0,前n项和有最小值
<0,d>0,前n项和有最小值 可由
可由 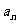 ≤0,且
≤0,且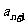 ≥0,求得n的值
≥0,求得n的值
(2)利用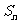 :由
:由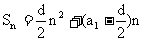 二次函数配方法求得最值时n的值
二次函数配方法求得最值时n的值
[精典范例]
[例1]已知一个等差数列的前四项和为21,末四项和为67,前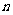 项和为286,求数列的项数
项和为286,求数列的项数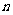 。
。
分析 条件中的8项可分为4组,每组中的两项与数列的首、尾两项等距。
[解]
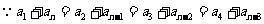
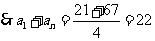 ,
,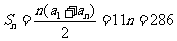 ,
,
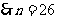 。
。
 [例2]已知两个等差数列{an}、{bn},它们的前n项和分别是Sn、Sn′,若
[例2]已知两个等差数列{an}、{bn},它们的前n项和分别是Sn、Sn′,若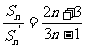 ,求
,求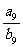 .
.
[解法一] ∵2a9=a1+a17,
2b9=b1+b17,∴S17=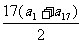 =17a9,
=17a9,
S17′=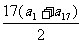 =17b9,∴
=17b9,∴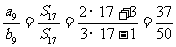 .
.
[解法二] ∵{an}、{bn}是等差数列,∴可设Sn=An2+Bn,Sn′=A’n2+B′
n(A、B、A′、B′∈R),∵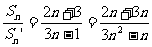 ,
,
进而可设Sn=(2n2+3n)t,
Sn′=(3n2-n)t(t∈R,t≠0),∴an=Sn-Sn-1=(2n2+3n)t-[2(n-1)2+3(n-1)t]=(4n+1)t,
∴a9=37t.
同理可得bn=Sn′-Sn-1′=(3n2-n)t-[3(n-1)2-(n-1)]t =(6n-4)t,
∴b9=50t,∴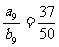 .
.
[例3]数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负.
(1)求数列的公差.
(2)求前n项和Sn的最大值.
(3)当Sn>0时,求n的最大值.
[解] (1)由已知a6=a1+5d=23+5d>0,a7=a1+6d=23+6d<0,
解得:-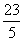 <d<-
<d<-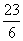 ,又d∈Z,∴d=-4
,又d∈Z,∴d=-4
(2)∵d<0,∴{an}是递减数列,又a6>0,a7<0∴当n=6时,Sn取得最大值,S6=6×23+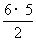 (-4)=78
(-4)=78
(3)Sn=23n+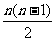 (-4)>0,整理得: n(50-4n)>0 ∴0<n<
(-4)>0,整理得: n(50-4n)>0 ∴0<n<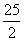 ,又n∈N*,
,又n∈N*,
所求n的最大值为12.
点评: 可将本题中的公差为整数的条件去掉,再考虑当n为何值时,数列{an}的前n项和取到最大值.
[例4]等差数列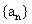 中,
中,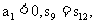 该数列的前多少项和最小?
该数列的前多少项和最小?
思路1:
求出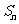 的函数解析式(n的二次函数,
的函数解析式(n的二次函数,
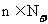 ),再求函数取得最小值时的n值.
),再求函数取得最小值时的n值.
思路2:
公差不为0的等差数列等差数列前n项和最小的条件为: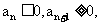
思路3:
由s9=s12得s12-s9=a10+a11+a12=0得a11=0.
思维点拔:
说明:根据项的值判断前 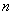 项和的最值有以下结论:
项和的最值有以下结论:
①当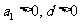 时,
时,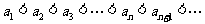 ,
,
则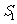 最小;
最小;
②当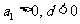 时,
时,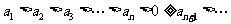 ,
,
则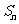 最大;
最大;
③当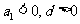 时,
时,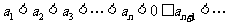 ,
,
则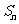 最小;
最小;
④当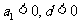 时,
时,
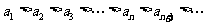 ,
,
则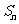 最大
最大
[追踪训练一]
2.在等差数列{an}中,若a1>0,d<0,则Sn存在最大值.若a1<0,d>0,则Sn存在最小值.
1. 等差数列{an}的公差为d,前n项和为Sn,那么数列Sk,S2k-Sk,S3k-S2k……(k∈N*)成等差数列,公差为k2d.
2.了解等差数列的一些性质,并会用它们解决一些相关问题
[自学评价]
1.进一步熟练掌握等差数列的通项公式和前n项和公式.
4. 一个等差数列,前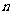 项的和为25,前
项的和为25,前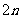 项的和为100,求前
项的和为100,求前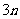 项的和.
项的和.
 [解]
[解]
[答案]前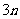 项的和为225
项的和为225
|
3.已知数列{an}的前n项和Sn=n2+2n+5,则a6+a7+a8=__45____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com