
1.等比数列{an}的首项为1,公比为q,前n项和为S,则数列{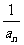 }的前n项之和为(
)
}的前n项之和为(
)
A.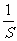 B.S C.
B.S C.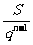 D.
D.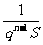
5.求和1-2+3-4+5-6+…+(-1)n+1n.
[解]
[选修延伸]
[例3]已知数列{an}中, an+1=an+2n,
a1=3,求an.
[解]
点评:利用数列的求和,可求出一些递推关系为an+1=an+f(n)的数列的通项公式.
[例4]已知{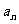 }为等比数列,且
}为等比数列,且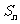 =a,
=a,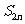 =b,(ab≠0),求
=b,(ab≠0),求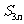 .
.
[解]
追踪训练二
4.数列1,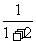 ,
,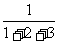 ,…,
,…,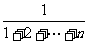 的前
的前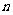 项和为( )
项和为( )
A.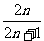 B.
B. 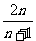
C.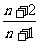 D.
D. 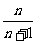
3.若数列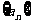 的通项公式为
的通项公式为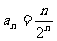 ,则前
,则前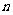 项和为( )
项和为( )
A.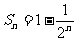 B.
B.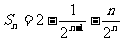 C.
C.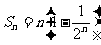 D.
D.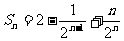
2.求和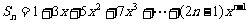
1. 求和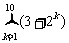
6.在等比数列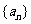 中,当项数为偶数
中,当项数为偶数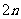 时,
时,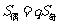 ;项数为奇数
;项数为奇数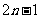 时,
时,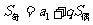
[精典范例]
[例1]求数列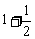 ,
,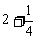 ,
,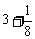 ,...的前n项和.
,...的前n项和.
分析:这个数列的每一项都是一个等差数列与一个等比数列的对应项的和,因此可以分组求和法.
 [解]
[解]
[例2]设数列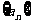 为
为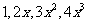 ,
, ,
,
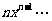
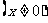 求此数列前
求此数列前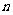 项的和.
项的和.
分析:这个数列的每一项都是一个等差数列与一个等比数列的对应项的积,因此可以用错项相减法.
[解]
追踪训练一
5.倒序相加法
4.裂项法:求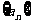 的前
的前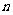 项和时,若能将
项和时,若能将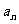 拆分为
拆分为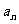 =
=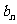 -
-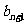 ,则
,则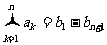
3.错位相减法:适用于{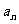
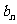 }的前
}的前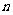 项和,其中
项和,其中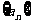 是等差数列,
是等差数列, 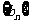 是等比数列;
是等比数列;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com