
1. 求下列等比数列的公比、第5项和第n项:
(1)2,6,18,54,…;
(2)7,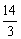 ,
,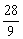 ,
,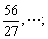
(3)0.3,-0.09,0.027,-0.0081,…;
(4)5,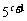 ,
,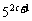 ,
,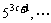 .
.
[答案]
(1) 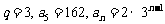
(2) 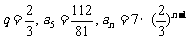
(3) 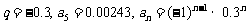
(4) 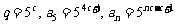
5.证明数列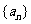 为等比数列:
为等比数列:
①定义:证明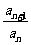 =常数,
=常数,
②中项性质: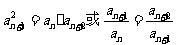 ;
;
[精典范例]
[例1]判断下列数列是否为等比数列:
(1)1,1,1,1,1;
(2)0,1,2,4,8;
(3)1,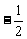 ,
,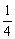 ,
,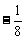 ,
,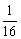 .
.
[解]
 (1)所给数列是首项为1,公比为1的等比数列.
(1)所给数列是首项为1,公比为1的等比数列.
(2)因为0不能作除数,所以这个数列不是等比数列.
(3)所给数列是首项为1,公比为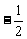 的等比数列.
的等比数列.
[例2]求出下列等比数列中的未知项:
(1)2,a,8;
(2)-4,b,c,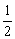 .
.
[解]
(1) 根据题意,得
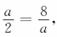
所以a=4或a=-4.
(2) 根据题意,得
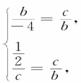
解得
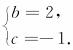
所以b=2,c=-1.
[例3]在等比数列{an}中,
(1)已知a1=3,q=-2,求a6;
(2)已知a3=20,a6=160,求an.
[解]
(1)由等比数列的通项公式,得
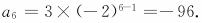
(2)设等比数列的公比为q,那么
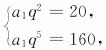
所以
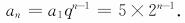
[例4]在243和3中间插入3个数,使这5个数成等比数列.
[解]设插入的三个数为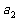 ,
,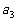 ,
,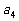 ,由题意知243,
,由题意知243,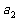 ,
,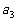 ,
,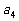 ,3成等比数列.
,3成等比数列.
设公比为q,则
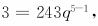
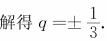
因此,所求三个数为81,27,9,
或-81,27,-9.
追踪训练一
4.等比中项的定义:如果a、G、b成等比数列,那么G叫做a与b的等比中项.且 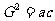
3.既是等差又是等比数列的数列:非零常数列.
2.等比数列的通项公式
① 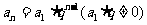
②
1.等比数列:一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q表示(q≠0),即: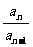 =q(q≠0)
=q(q≠0)
注:1°“从第二项起”与“前一项”之比为常数q
{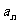 }成等比数列
}成等比数列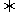
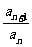 =q(
=q(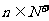 ,q≠0)
,q≠0)
2° 隐含:任一项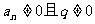
3° q= 1时,{an}为常数列.
3. 掌握等比数列的通项公式,并能运用公式解决一些简单的实际问题.
[自学评价]
2.类比等差数列的通项公式,探索发现等比数列的通项公式, 掌握求等比数列通项公式的方法,
1.体会等比数列是用来刻画一类离散现象的重要数学模型,理解等比数列的概念,
5.已知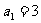 ,
,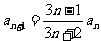
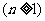 ,求
,求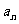 .
.
[解]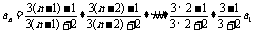
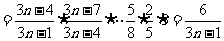
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com