
2.等比数列{an}中,a3=7,前 3项之和S3=21, 则公比q的值为( C )
A.1
B.-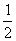
C.1或-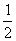 D.-1或
D.-1或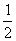
1.在等比数列{an}中,Sn表示前n项和,若a3=2S2+1,a4=2S3+1,则公比q等于( A )
A.3 B.-3 C.-1 D.1
5.已知等比数列的公比为2,若前4项之和等于1,则前8项之和等于( B )
A.15 B.17 C.19 D.21
[选修延伸]
[例4]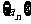 是等比数列,
是等比数列,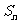 是其前n项和,数列
是其前n项和,数列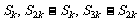 (
(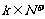 )是否仍成等比数列?
)是否仍成等比数列?
[解]
设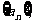 首项是
首项是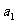 ,公比为q,
,公比为q,
①当q=-1且k为偶数时,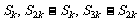 不是等比数列.
不是等比数列.
∵此时,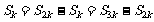 =0.
=0.
例如:数列1,-1,1,-1,…是公比为-1的等比数列,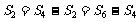 S2=0,
S2=0,
②当q≠-1或k为奇数时,
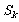 =
=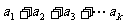
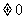
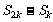 =
=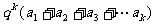
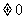
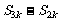 =
=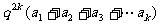
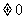

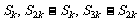 (
(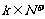 )成等比数列
)成等比数列
追踪训练二
4.若等比数列{an}的前n项之和Sn=3n+a,则a等于( D )
A.3 B.1 C.0 D.-1
3.等比数列{an}的各项都是正数,若a1=81,a5=16,则它的前5项和是( B )
A.179 B.211 C.243 D.275
2.求下列等比数列的各项和:
(1)1,3,9,…,2187;
(2)1,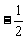 ,
,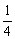 ,
,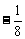 ,…,
,…,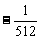 .
.
[答案](1)3280;(2)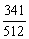
1.某厂去年的产值记为1,计划在今后五年内每年的产值比上年增长10%,则从今年起到第五年,这个厂的总产值为(C).
A.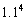 B.
B.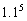
C.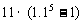 D.
D.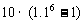
2.若数列{an}的前n项和Sn=p(1-qn),且p≠0,q≠1,则数列{an}是等比数列.
[精典范例]
[例1]在等比数列{an}中,
(1)已知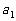 =-4,
=-4,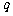 =12,求
=12,求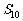 ;
;
(2)已知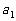 =1,
=1,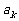 =243,
=243,
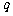 =3,求
=3,求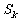 .
.
[解]
(1)根据等比数列的前n项和公式,得
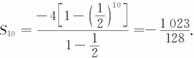
(2)根据等比数列的前n项和公式,得
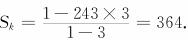
[例2]在等比数列{an}中,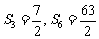 ,求an.
,求an.
 [解]若q=1,则S6=2S3,这与已知
[解]若q=1,则S6=2S3,这与已知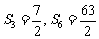 是矛盾的,所以q≠1.从而
是矛盾的,所以q≠1.从而
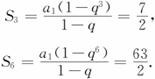
将上面两个等式的两边分别相除,得
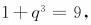
所以q=2,由此可得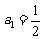 ,因此
,因此
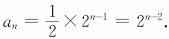
点评:等比数列中五个基本量a1、q、an、n、Sn,知三可求二.
[例3]在等比数列{an}中,a1+an=66,a2·an-1=128,且前n项和Sn=126,求n及公比q.
[解] ∵a1an=a2an-1=128,又a1+an=66,
∴a1、an是方程x2-66x+128=0的两根,
解方程得x1=2,x2=64,
∴a1=2,an=64或a1=64,an=2,显然q≠1.
若a1=2,an=64,由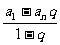 =126
=126
得2-64q=126-126q,
∴q=2,
由an=a1qn-1得2n-1=32,
∴n=6.
若a1=64,an=2,同理可求得q=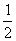 ,n=6.
,n=6.
综上所述,n的值为6,公比q=2或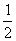 .
.
点评:等比数列中五个基本量a1、q、an、n、Sn,知三可求二,列方程组是求解的常用方法.解本题的关键是利用a1an=a2an-1,进而求出a1、an,要注意a1、an是两组解.
追踪训练一
1.等比数列{an}的前n项和为Sn
当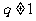 时,
时,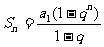 ①
①
或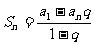 ②
②
当q=1时,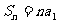
当已知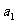 , q, n 时用公式①;
, q, n 时用公式①;
当已知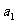 , q,
, q, 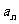 时,用公式②.
时,用公式②.
2.会用等比数列的前n项和公式解决有关等比数列的一些简单问题
[自学评价]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com