
7.在一个以AB为弦的弓形中,C为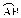 的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求
的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求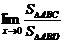 .
.
解:设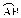 所在圆圆心为O,则C、D、O都在AB的中垂线上,
所在圆圆心为O,则C、D、O都在AB的中垂线上,
∴∠AOD=∠BOD=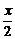 .设OA=r.
.设OA=r.
S△ABC=S四边形AOBC-S△AOB=r2sin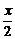 -
-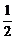 r2sinx=r2sin
r2sinx=r2sin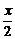 (1-cos
(1-cos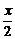 ),
),
S△ABD=S四边形AOBD-S△AOB=r2tan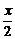 -
-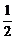 r2sinx=r2
r2sinx=r2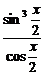 .
.
∴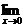
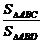 =
=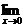
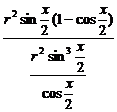 =
=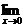
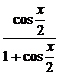 =
=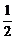 .
.
6.设函数f (x)=ax2+bx+c是一个偶函数,且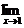 f (x)=0,
f (x)=0,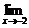 f (x)=-3,求出这一函数最大值.
f (x)=-3,求出这一函数最大值.
解:∵f (x)=ax2+bx+c是一偶函数,
∴f (-x)=f (x),
即ax2+bx+c=ax2-bx+c.
∴b=0.∴f (x)=ax2+c.
又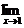 f (x)=
f (x)= 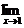 ax2+c=a+c=0,
ax2+c=a+c=0, 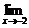 f(x)=
f(x)=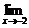 ax2+c=4a+c=-3,
ax2+c=4a+c=-3,
∴a=-1,c=1.
∴f (x)=-x2+1.
∴f (x)max=f(0)=1.
∴f (x)的最大值为1.
培养能力
5.已知函数f (x)=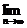
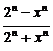 ,试求:
,试求:
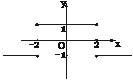
(1)f (x)的定义域,并画出图象;
(2)求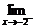 f (x)、
f (x)、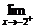 f (x),并指出
f (x),并指出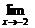 f (x)是否存在.
f (x)是否存在.
解:(1)当|x|>2时,
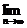
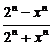 =
=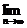
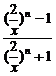 =-1;
=-1;
当|x|<2时,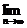
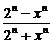 =
=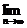
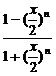 =1;
=1;
当x=2时,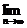
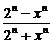 =0;
=0;
当x=-2时,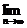
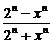 不存在.
不存在.
∴f (x)=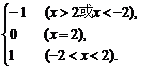
∴f (x)的定义域为{x|x<-2或x=2或x>2}.
如下图:
(2)∵ f (x)=-1,
f (x)=-1,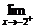 f (x)=1.∴
f (x)=1.∴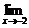 f (x)不存在.
f (x)不存在.
4.若f (x)=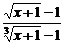 在点x=0处连续,则f
(0)=__________________.
在点x=0处连续,则f
(0)=__________________.
解析:∵f(x)在点x=0处连续,
∴f (0)=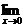 f (x),
f (x),
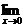 f (x)=
f (x)= 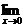
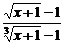
= 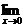
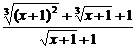 =
=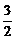 .
.
答案: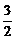
3.已知函数y=f (x)在点x=x0处存在极限,且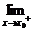 f (x)=a2-2,
f (x)=a2-2,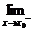 f (x)=2a+1,则函数y=f (x)在点x=x0处的极限是____________.
f (x)=2a+1,则函数y=f (x)在点x=x0处的极限是____________.
解析:∵y=f(x)在x=x0处存在极限,
∴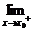 f(x)=
f(x)=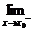 f(x),即a2-2=2a+1.∴a=-1或a=3.
f(x),即a2-2=2a+1.∴a=-1或a=3.
∴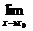 f (x)=2a+1=-1或7.
f (x)=2a+1=-1或7.
答案:-1或7
2.(2004年全国Ⅱ,理2)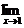
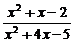 等于
等于
A.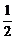 B.1
C.
B.1
C.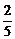 D.
D.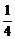
解析:∵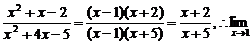
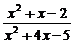 =
=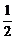 .
.
答案:A
1.已知函数f (x)是偶函数,且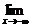 f (x)=a,则下列结论一定正确的是
f (x)=a,则下列结论一定正确的是
A. 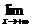 f (x)=-a
B.
f (x)=-a
B. 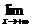 f (x)=a
f (x)=a
C. 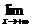 f (x)=|a|
D.
f (x)=|a|
D. 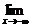 f(x)=|a|
f(x)=|a|
解析:∵f (x)是偶函数,∴f (-x)=f(x).
又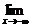 f (x)=a,
f (x)=a,
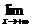 f(-x)=a,f (x)=f
(-x),
f(-x)=a,f (x)=f
(-x),
∴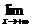 f(-x)=
f(-x)= 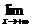 f (x)=a.
f (x)=a.
答案:B
5.若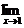
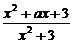 =2,则a=__________.
=2,则a=__________.
解析: 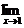
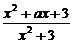 =2,
=2,
∴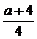 =2.∴a=4.
=2.∴a=4.
答案:4
●典例剖析
[例1]求下列各极限:
(1) 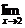 (
(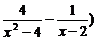 ;
;
(2)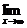 (
(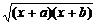 -x);
-x);
(3) 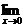
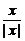 ;
;
(4) 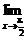
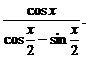
剖析:若f
(x)在x0处连续,则应有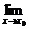 f (x)=f (x0),故求f
(x)在连续点x0处的极限时,只需求f
(x0)即可;若f (x)在x0处不连续,可通过变形,消去x-x0因式,转化成可直接求f(x0)的式子.
f (x)=f (x0),故求f
(x)在连续点x0处的极限时,只需求f
(x0)即可;若f (x)在x0处不连续,可通过变形,消去x-x0因式,转化成可直接求f(x0)的式子.
解:(1)原式=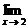
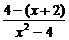 =
=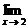
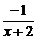 =-
=-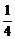 .
.
(2)原式=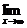
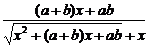 =a+b.
=a+b.
(3)因为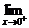
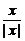 =1,而=
=1,而=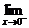
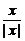 =-1,
=-1,
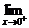
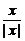 ≠
≠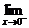
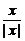 ,
,
所以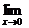
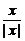 不存在.
不存在.
(4)原式=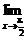
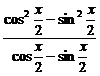 =
=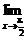 (cos
(cos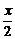 +sin
+sin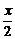 )=
)=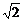 .
.
思考讨论
数列极限与函数极限的区别与联系是什么?
[例2] (1)设f(x)=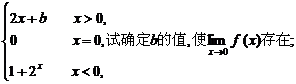 ;
;
(2)f
(x)为多项式,且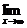
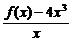 =1,
=1,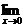
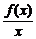 =5,求f(x)的表达式.
=5,求f(x)的表达式.
解:(1)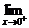 f (x)=
f (x)= 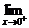 (2x+b)=b,
(2x+b)=b,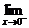 f(x)=
f(x)= 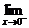 (1+2x)=2,
(1+2x)=2,
当且仅当b=2时,
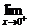 f (x)=
f (x)= 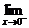 f (x),
f (x),
故b=2时,原极限存在.
(2)由于f(x)是多项式,且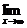
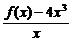 =1,
=1,
∴可设f (x)=4x3+x2+ax+b(a、b为待定系数).
又∵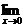
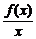 =5,
=5,
即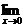 (4x2+x+a+
(4x2+x+a+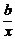 )=5,
)=5,
∴a=5,b=0,即f (x)=4x3+x2+5x.
评述:(1)函数在某点处有极限,与其在该点处是否连续不同.
(2)初等函数在其定义域内每点的极限值就等于这一点的函数值,也就是对初等函数而言,求极限就是求函数值,使极限运算大大简化.
[例3] 讨论函数f (x)= 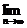
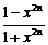 ·x (0≤x<+∞)的连续性,并作出函数图象.
·x (0≤x<+∞)的连续性,并作出函数图象.
部析:应先求出f (x)的解析式,再判断连续性.
解:当0≤x<1时,f (x)= 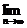
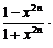 x=x;
x=x;
当x>1时,f (x)= 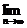
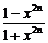 ·x=
·x=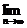
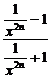 ·x=-x;
·x=-x;
当x=1时,f (x)=0.
∴f (x)=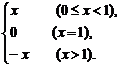 [i]
[i]
∵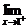 f(x)=
f(x)=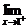 (-x)=-1,
(-x)=-1,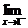 f(x)=
f(x)= 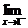 x=1,
x=1,
∴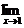 f(x)不存在.
f(x)不存在.
∴f (x)在x=1处不连续,f (x)在定义域内的其余点都连续.
图象如下图所示.
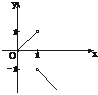
评述:分段函数讨论连续性,一定要讨论在“分界点”的左、右极限,进而判断连续性.
●闯关训练
夯实基础
4.(2005年西城区抽样测试)
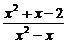 =________________.
=________________.
解析: 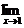
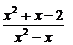 =
=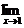
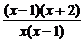 =
=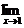
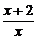 =3.
=3.
答案:3
3.函数f(x)在x0处连续是f(x)在点x0处有极限的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com