
2.f(x)=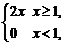 下列结论正确的是
下列结论正确的是
A.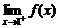 =
=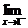 f(x)
f(x)
B.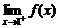 =2,
=2,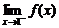 不存在
不存在
C.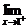 f (x)=0,
f (x)=0, 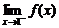 不存在
不存在
D.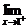 f (x)≠
f (x)≠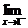 f (x)
f (x)
答案:D
1.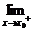 f(x)=
f(x)=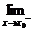 f(x)=a是f(x)在x0处存在极限的
f(x)=a是f(x)在x0处存在极限的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:C
2.极限的四则运算法则:
如果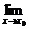 f (x)=a,
f (x)=a, 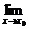 g(x)=b,那么
g(x)=b,那么
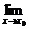 [f(x)±g(x)]=a±b;
[f(x)±g(x)]=a±b; 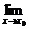 [f(x)·g(x)]=a·b;
[f(x)·g(x)]=a·b; 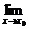
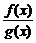 =
=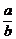 (b≠0).
(b≠0).
特别提示
(1)上述法则对x→∞的情况仍成立;
(2)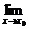 [Cf(x)]=C
[Cf(x)]=C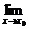 f(x)(C为常数);
f(x)(C为常数);
(3)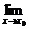 [f(x)]n=[
[f(x)]n=[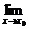 f(x)]n(n∈N *).
f(x)]n(n∈N *).
●点击双基
1.函数极限的概念:(1)如果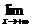 f(x)=a且
f(x)=a且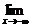 f(x)=a,那么就说当x趋向于无穷大时,函数f(x)的极限是a,记作
f(x)=a,那么就说当x趋向于无穷大时,函数f(x)的极限是a,记作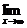 f(x)=a,也可记作当x→∞时,f(x)→a.
f(x)=a,也可记作当x→∞时,f(x)→a.
(2)一般地,当自变量x无限趋近于常数x0(但x不等于x0)时,如果函数f(x)无限趋近于一个常数a,就说当x趋近于x0时,函数f(x)的极限是a,记作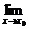 f(x)=a,也可记作当x→x0时,f(x)→a.
f(x)=a,也可记作当x→x0时,f(x)→a.
(3)一般地,如果当x从点x=x0左侧(即x<x0)无限趋近于x0时,函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处的左极限,记作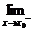 f (x)=a.如果从点x=x0右侧(即x>x0)无限趋近于x0时,函数f
(x)无限趋近于常数a,就说a是函数 f (x)在点x0处的右极限,记作
f (x)=a.如果从点x=x0右侧(即x>x0)无限趋近于x0时,函数f
(x)无限趋近于常数a,就说a是函数 f (x)在点x0处的右极限,记作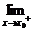 f(x)=a.
f(x)=a.
13.3 函数的极限
●知识梳理
2.重视在日常学习过程中化归思想、分类讨论思想和极限思想的运用.
拓展题例
[例题] 已知等比数列{an}的首项为a1,公比为q,且有 (
(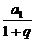 -qn)=
-qn)=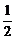 ,求首项a1的取值范围.
,求首项a1的取值范围.
解:  (
(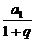 -qn)=
-qn)=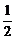 ,
,
∴ qn一定存在.∴0<|q|<1或q=1.
qn一定存在.∴0<|q|<1或q=1.
当q=1时,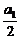 -1=
-1=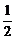 ,∴a1=3.
,∴a1=3.
当0<|q|<1时,由 (
(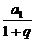 -qn)=
-qn)=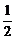 得
得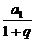 =
=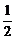 ,∴2a1-1=q.
,∴2a1-1=q.
∴0<|2a1-1|<1.∴0<a1<1且a1≠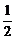 .
.
综上,得0<a1<1且a1≠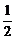 或a1=3.
或a1=3.
1.数列极限的几种类型:∞-∞,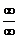 ,0-0,
,0-0,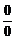 等形式,必须先化简成可求极限的类型再用四则运算求极限,另外还有先求和,约分后再求极限,对含参数的题目一定要控制好难度,不要太难了.
等形式,必须先化简成可求极限的类型再用四则运算求极限,另外还有先求和,约分后再求极限,对含参数的题目一定要控制好难度,不要太难了.
2.熟练掌握如下几个常用极限:
(1)  C=C(C为常数);
C=C(C为常数);
(2)  (
(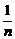 )p=0(p>0);
)p=0(p>0);
(3) 
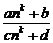 =
=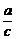 (k∈N *,a、b、c、d∈R且c≠0);
(k∈N *,a、b、c、d∈R且c≠0);
(4)  qn=0(|q|<1).
qn=0(|q|<1).
●教师下载中心
教学点睛
1.运用数列极限的运算法则求一些数列的极限时必须注意以下几点:
(1)各数列的极限必须存在;
(2)四则运算只限于有限个数列极限的运算.
9.已知数列{an}满足a1=0,a2=1,an=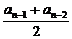 ,求
,求 an.
an.
解:由an=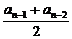 ,得
,得
2an+an-1=2an-1+an-2,∴{2an+an-1}是常数列.
∵2a2+a1=2,∴2an+an-1=2.
∴an-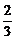 =-
=-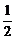 (an-1-
(an-1-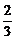 ).
).
∴{an-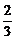 }是公比为-
}是公比为-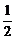 ,首项为-
,首项为-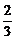 的等比数列.
的等比数列.
∴an-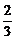 =-
=-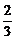 ×(-
×(-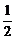 )n-1.
)n-1.
∴an=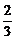 -
-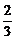 ×(-
×(-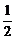 )n-1.
)n-1.
∴ an=
an=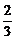 .
.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com