
3.已知函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的范围是
A.f(1)≥25 B.f(1)=25
C.f(1)≤25 D.f(1)>25
解析:由y=f(x)的对称轴是x=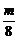 ,可知f(x)在[
,可知f(x)在[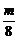 ,+∞)上递增,由题设只需
,+∞)上递增,由题设只需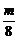 ≤-2
≤-2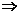 m≤-16,
m≤-16,
∴f(1)=9-m≥25.
答案:A
2.二次函数y=x2-2(a+b)x+c2+2ab的图象的顶点在x轴上,且a、b、c为△ABC的三边长,则△ABC为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
解析:y=[x-(a+b)]2+c2+2ab-(a+b)2=[x-(a+b)]2+c2-a2-b2.
∴顶点为(a+b,c2-a2-b2).
由题意知c2-a2-b2=0.
∴△ABC为直角三角形.
答案:B
1.设二次函数f(x)=ax2+bx+c(a≠0),如果f(x1)=f(x2)(其中x1≠x2),则f(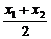 )等于
)等于
A.-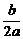 B.-
B.-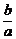
C.c D.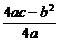
解析:f(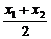 )=f(-
)=f(-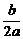 )=
)=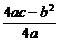 .
.
答案:D
2.6 二次函数
●知识梳理
二次函数的基本性质
(1)二次函数的三种表示法:
y=ax2+bx+c;y=a(x-x1)(x-x2);y=a(x-x0)2+n.
(2)当a>0,f(x)在区间[p,q]上的最大值为M,最小值为m,令x0=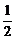 (p+q).
(p+q).
若-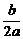 <p,则f(p)=m,f(q)=M;
<p,则f(p)=m,f(q)=M;
若p≤-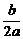 <x0,则f(-
<x0,则f(-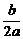 )=m,f(q)=M;
)=m,f(q)=M;
若x0≤-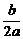 <q,则f(p)=M,f(-
<q,则f(p)=M,f(-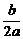 )=m;
)=m;
若-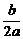 ≥q,则f(p)=M,f(q)=m.
≥q,则f(p)=M,f(q)=m.
●点击双基
4.分段函数的反函数,应分别求出各段的反函数,再合成.
●教师下载中心
教学点睛
由于本节中的反函数的定义既是重点又是难点,因此复习本节时,针对反函数的定义,教师应渗透如下知识:
(1)函数的反函数,本身也是一个函数,由反函数的定义,原来函数也是反函数的反函数.
(2)反函数的定义域、值域分别是原来函数的值域与定义域.
(3)由反函数定义知:①b=f(a)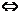 a=f-1(b),这两个式子是a、b之间关系的两种不同表示形式.
a=f-1(b),这两个式子是a、b之间关系的两种不同表示形式.
②f[f-1(x)]=x(x∈C).
③f-1[f(x)]=x(x∈A).
拓展题例
[例1] (2004年上海,10)若函数y=f(x)的图象可由y=lg(x+1)的图象绕坐标原点O逆时针旋转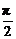 得到,则f(x)等于
得到,则f(x)等于
A.10-x-1 B.10x-1 C.1-10-x D.1-10x
解析:所求函数与y=lg(x+1)的反函数的图象关于y轴对称.
答案:A
[例2] 若函数y=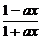 (x≠-
(x≠-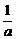 ,x∈R)的图象关于直线y=x对称,求a的值.
,x∈R)的图象关于直线y=x对称,求a的值.
解法一:由y=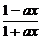 ,解得x=
,解得x=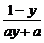 .故函数y=
.故函数y=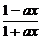 的反函数为y=
的反函数为y=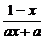 .
.
∵函数y=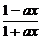 的图象关于直线y=x对称,
的图象关于直线y=x对称,
∴函数y=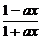 与它的反函数y=
与它的反函数y=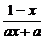 相同.由
相同.由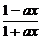 =
=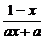 恒成立,得a=1.
恒成立,得a=1.
解法二:∵点(0,1)在函数y=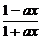 的图象上,且图象关于直线y=x对称,
的图象上,且图象关于直线y=x对称,
∴点(0,1)关于直线y=x的对称点(1,0)也在原函数图象上,代入得a=1.
[例3] 函数y=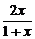 (x∈(-1,+∞))的图象与其反函数图象的交点坐标为___________________.
(x∈(-1,+∞))的图象与其反函数图象的交点坐标为___________________.
答案:(0,0),(1,1)
3.求y=f(x)的反函数的一般步骤:
(1)确定原函数的值域,也就是反函数的定义域;
(2)由y=f(x)的解析式求出x=f-1(y);
(3)将x、y对换,得反函数的习惯表达式y=f-1(x).
2.互为反函数的两个函数具有相同的增减性,它们的图象关于直线y=x对称.
1.反函数的定义域和值域分别是原函数的值域和定义域,因此反函数的定义域不能由其解析式确定,而应当是原函数的值域.
10.已知函数f(x)=(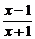 )2(x>1).
)2(x>1).
(1)求f(x)的反函数f-1(x);
(2)判定f-1(x)在其定义域内的单调性;
(3)若不等式(1-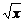 )f-1(x)>a(a-
)f-1(x)>a(a-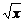 )对x∈[
)对x∈[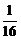 ,
,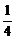 ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
解:(1)由y=(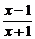 )2,得x=
)2,得x=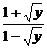 .
.
又y=(1-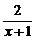 )2,且x>1,∴0<y<1.
)2,且x>1,∴0<y<1.
∴f-1(x)=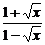 (0<x<1).
(0<x<1).
(2)设0<x1<x2<1,则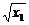 -
-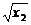 <0,1-
<0,1-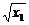 >0,1-
>0,1-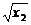 >0.
>0.
∴f-1(x1)-f-1(x2)=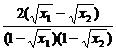 <0,即f-1(x1)<f-1(x2).
<0,即f-1(x1)<f-1(x2).
∴f-1(x)在(0,1)上是增函数.
(3)由题设有(1-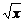 )
)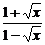 >a(a-
>a(a-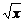 ).
).
∴1+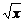 >a2-a
>a2-a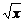 ,即(1+a)
,即(1+a)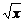 +1-a2>0对x∈[
+1-a2>0对x∈[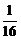 ,
,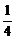 ]恒成立.显然a≠-1.令t=
]恒成立.显然a≠-1.令t=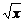 ,∵x∈[
,∵x∈[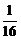 ,
,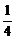 ],∴t∈[
],∴t∈[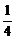 ,
,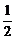 ].
].
则g(t)=(1+a)t+1-a2>0对t∈[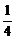 ,
,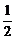 ]恒成立.
]恒成立.
由于g(t)=(1+a)t+1-a2是关于t的一次函数,∴g(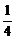 )>0且g(
)>0且g(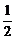 )>0,即
)>0,即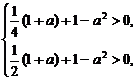 解得-1<a<
解得-1<a<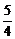 .
.
评述:本题(3)巧用换元法,通过构造一次函数,借助函数图象求解.
●思悟小结
9.已知函数f(x)=2(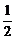 -
-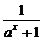 )(a>0,且a≠1).
)(a>0,且a≠1).
(1)求函数y=f(x)的反函数y=f-1(x);
(2)判定f-1(x)的奇偶性;
(3)解不等式f-1(x)>1.
解:(1)化简,得f(x)=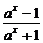 .
.
设y=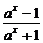 ,则ax=
,则ax=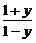 .∴x=loga
.∴x=loga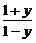 .
.
∴所求反函数为
y=f-1(x)=loga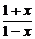 (-1<x<1).
(-1<x<1).
(2)∵f-1(-x)=loga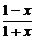 =loga(
=loga(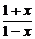 )-1=-loga
)-1=-loga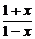 =-f-1(x),
=-f-1(x),
∴f-1(x)是奇函数.
(3)loga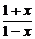 >1.
>1.
当a>1时,
原不等式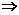
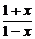 >a
>a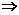
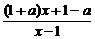 <0.
<0.
∴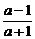 <x<1.
<x<1.
当0<a<1时,原不等式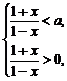
解得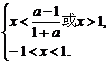
∴-1<x<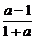 .
.
综上,当a>1时,所求不等式的解集为(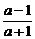 ,1);
,1);
当0<a<1时,所求不等式的解集为(-1,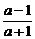 ).
).
探究创新
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com