5.若函数f(x)=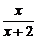，则f^－1()=___________.

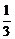解法一：由f(x)=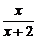，得f^－1(x)=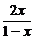.∴f^－1(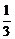)==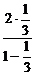1.

解法二：由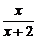=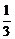，解得x=1.

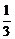∴f^－1()=1.

答案：1

评述：显然解法二更简便.

●典例剖析

[例1] 设函数f(x)是函数g(x)=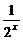的反函数，则f(4－x²)的单调递增区间为

A.［0，+∞)　　　　 　　　　　　　　　　　　　　　　　 B.(－∞，0］

C.［0，2)　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－2，0］

解析：f(4－x²)=－log₂(4－x²).x∈(－2，0］时，4－x²单调递增；x∈［0，2)时，4－x²单调递减.

答案：C

深化拓展

4.(2005年春季上海，4)函数f(x)=－x²(x∈(－∞，－2］)的反函数f^－1(x)=______________.

解析：y=－x²(x≤－2)，y≤－4.

∴x=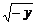－.x、y互换，

∴f^－1(x)=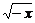－(x≤－4).

答案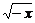：－(x≤－4)

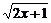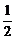3.函数f(x)=－(x≥－)的反函数

A.在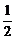［－，+∞)上为增函数　　　　　　　　　　　 B.在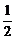［－，+∞)上为减函数

C.在(－∞，0］上为增函数　　　　　　　　　　　　　 D.在(－∞，0］上为减函数

解析：函数f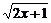(x)=－(x≥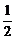－)的值域为{y|y≤0}，而原函数在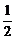［－，+∞)上是减函数，所以它的反函数在(－∞，0］上也是减函数.

答案：D

2.函数y=log₂(x+1)+1(x＞0)的反函数为

A.y=2^x－1－1(x＞1)　　　　　　　　　　　　　　　　　　　 B.y=2^x－1+1(x＞1)

C.y=2^x+1－1(x＞0)　　　　　　　　　　　　　　　　　　　 D.y=2^x+1+1(x＞0)

解析：函数y=log₂(x+1)+1(x＞0)的值域为{y|y＞1}，由y=log₂(x+1)+1，解得x=2^y－1－1.

∴函数y=log₂(x+1)+1(x＞0)的反函数为y=2^x－1－1(x＞1).

答案：A

1.(2005年北京东城区模拟题)函数y=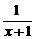－(x≠－1)的反函数是

A.y=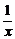－－1(x≠0)　　　　　　　　　　　　　　　　　　 B.y=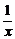－+1(x≠0)

C.y=－x+1(x∈R)　　　　　　　　　　　　　　　　　　　　 D.y=－x－1(x∈R)

解析：y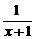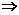=－(x≠－1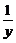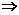)x+1=－x=－1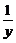－.x、y交换位置，得y=－1－.

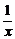答案：A

3.求反函数的步骤：

(1)解关于x的方程y=f(x)，得到x=f^－1(y).

(2)把第一步得到的式子中的x、y对换位置，得到y=f^－1(x).

(3)求出并说明反函数的定义域(即函数y=f(x)的值域).

●点击双基

2.互为反函数的两个函数y=f(x)与y=f^－1(x)在同一直角坐标系中的图象关于直线y=x对称.

1.反函数定义：若函数y=f(x)(x∈A)的值域为C，由这个函数中x、y的关系，用y把x表示出来，得到x=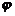(y).如果对于y在C中的任何一个值，通过x=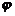(y)，x在A中都有唯一的值和它对应，那么，x=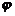(y)就表示y是自变量，x是自变量y的函数.这样的函数x=(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作x=f^－1(y).

在函数x=f^－1(y)中，y表示自变量，x表示函数.习惯上，我们一般用x表示自变量，y表示函数，因此我们常常对调函数x=f^－1(y)中的字母x、y，把它改写成y=f^－1(x).

2.5　 反函数

●知识梳理

3.在教学过程中应强调函数的奇偶性是函数的整体性质，而单调性是其局部性质.

拓展题例

[例1] 已知函数f(x)=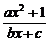(a、b、c∈Z)是奇函数，又f(1)=2，f(2)＜3，求a、b、c的值.

解：由f(－x)=－f(x)，得－bx+c=－(bx+c).

∴c=0.

由f(1)=2，得a+1=2b.

由f(2)＜3，得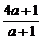＜3，

解得－1＜a＜2.又a∈Z，

∴a=0或a=1.若a=0，则b=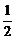，与b∈Z矛盾.∴a=1，b=1，c=0.

[例2] 已知函数y=f(x)的定义域为R，对任意x、x′∈R均有f(x+x′)=f(x)+f(x′)，且对任意x＞0，都有f(x)＜0，f(3)=－3.

(1)试证明：函数y=f(x)是R上的单调减函数；

(2)试证明：函数y=f(x)是奇函数；

(3)试求函数y=f(x)在［m，n］(m、n∈Z，且mn＜0)上的值域.

分析：(1)可根据函数单调性的定义进行论证，考虑证明过程中如何利用题设条件.

(2)可根据函数奇偶性的定义进行证明，应由条件先得到f(0)=0后，再利用条件f(x₁+x₂)=f(x₁)+f(x₂)中x₁、x₂的任意性，可使结论得证.

(3)由(1)的结论可知f(m)、f(n)分别是函数y=f(x)在［m、n］上的最大值与最小值，故求出f(m)与f(n)就可得所求值域.

(1)证明：任取x₁、x₂∈R，且x₁＜x₂，f(x₂)=f［x₁+(x₂－x₁)］，

于是由题设条件f(x+x′)=f(x)+f(x′)可知f(x₂)=f(x₁)+f(x₂－x₁).

∵x₂＞x₁，∴x₂－x₁＞0.∴f(x₂－x₁)＜0.

∴f(x₂)=f(x₁)+f(x₂－x₁)＜f(x₁).

故函数y=f(x)是单调减函数.

(2)证明：∵对任意x、x′∈R均有f(x+x′)=f(x)+f(x′)，

∴若令x=x′=0，则f(0)=f(0)+f(0).

∴f(0)=0.

再令x′=－x，则可得f(0)=f(x)+f(－x).

∵f(0)=0，∴f(－x)=－f(x).故y=f(x)是奇函数.

(3)解：由函数y=f(x)是R上的单调减函数，

∴y=f(x)在［m，n］上也为单调减函数.

∴y=f(x)在［m，n］上的最大值为f(m)，最小值为f(n).

∴f(n)=f［1+(n－1)］=f(1)+f(n－1)=2f(1)+f(n－2)=…=nf(1).

同理，f(m)=mf(1).

∵f(3)=－3，∴f(3)=3f(1)=－3.

∴f(1)=－1.∴f(m)=－m，f(n)=－n.

因此，函数y=f(x)在［m，n］上的值域为［－n，－m］.

评述：(1)满足题设条件f(x+x′)=f(x)+f(x′)的函数，只要其定义域是关于原点对称的，它就为奇函数.

(2)若将题设条件中的x＞0，均有f(x)＜0改成均有f(x)＞0，则函数f(x)就是R上的单调增函数.

(3)若题设条件中的m、n∈Z去掉，则我们就无法求出f(m)与f(n)的值，故m、n∈Z不可少.