
3.(2004年全国Ⅰ,5)(2x3-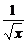 )7的展开式中常数项是
)7的展开式中常数项是
A.14 B.-14 C.42 D.-42
解析:设(2x3-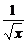 )7的展开式中的第r+1项是T
)7的展开式中的第r+1项是T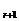 =C
=C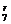 (2x3)
(2x3)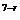 (-
(-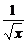 )r=C
)r=C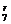 2
2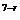 ·
·
(-1)r·x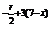 ,
,
当-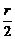 +3(7-r)=0,即r=6时,它为常数项,∴C
+3(7-r)=0,即r=6时,它为常数项,∴C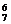 (-1)6·21=14.
(-1)6·21=14.
答案:A
2.(2004年江苏,7)(2x+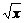 )4的展开式中x3的系数是
)4的展开式中x3的系数是
A.6 B.12 C.24 D.48
解析:(2x+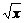 )4=x2(1+2
)4=x2(1+2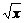 )4,在(1+2
)4,在(1+2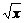 )4中,x的系数为C
)4中,x的系数为C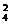 ·22=24.
·22=24.
答案:C
1.已知(1-3x)9=a0+a1x+a2x2+…+a9x9,则|a0|+|a1|+|a2|+…+|a9|等于
A.29 B.49 C.39 D.1
解析:x的奇数次方的系数都是负值,
∴|a0|+|a1|+|a2|+…+|a9|=a0-a1+a2-a3+…-a9.
∴已知条件中只需赋值x=-1即可.
答案:B
3.利用二项式展开式可以证明整除性问题,讨论项的有关性质,证明组合数恒等式,进行近似计算等.
●点击双基
2.二项展开式的性质是解题的关键.
1.二项展开式的通项公式是解决与二项式定理有关问题的基础.
10.5 二项式定理
●知识梳理
3.关于排列、组合问题的求解,应掌握以下基本方法与技巧
(1)特殊元素优先安排;(2)合理分类与准确分步;(3)排列、组合混合问题先选后排;(4)相邻问题捆绑处理;(5)不相邻问题插空处理;(6)定序问题排除法处理;(7)分排问题直排处理;(8)“小集团”排列问题先整体后局部;(9)构造模型;(10)正难则反,等价转化.
拓展题例
[例1] (1)一条长椅上有9个座位,3个人坐,若相邻2人之间至少有2个空椅子,共有几种不同的坐法?
(2)一条长椅上有7个座位,4个人坐,要求3个空位中,恰有2个空位相邻,共有多少种不同的坐法?
解:(1)先将3人(用×表示)与4张空椅子(用□表示)排列如图(×□□×□□×),这时共占据了7张椅子,还有2张空椅子,一是分开插入,如图中箭头所示(↓×□↓□×□↓□×↓),从4个空当中选2个插入,有C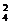 种插法;二是2张同时插入,有C
种插法;二是2张同时插入,有C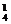 种插法,再考虑3人可交换有A
种插法,再考虑3人可交换有A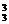 种方法.
种方法.
所以,共有A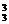 (C
(C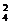 +C
+C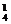 )=60(种).
)=60(种).
下面再看另一种构造方法:
先将3人与2张空椅子排成一排,从5个位置中选出3个位置排人,另2个位置排空椅子,有A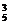 C
C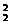 种排法,再将4张空椅子中的每两张插入每两人之间,只有1种插法,所以所求的坐法数为A
种排法,再将4张空椅子中的每两张插入每两人之间,只有1种插法,所以所求的坐法数为A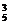 ·C
·C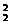 =60.
=60.
(2)可先让4人坐在4个位置上,有A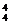 种排法,再让2个“元素”(一个是两个作为一个整体的空位,另一个是单独的空位)插入4个人形成的5个“空当”之间,有A
种排法,再让2个“元素”(一个是两个作为一个整体的空位,另一个是单独的空位)插入4个人形成的5个“空当”之间,有A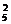 种插法,所以所求的坐法数为A
种插法,所以所求的坐法数为A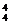 ·A
·A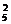 =480.
=480.
[例2] 已知1<m<n,m,n∈N*,求证:(1+m)n>(1+n)m.
证法一:由二项式定理(1+m)n=C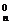 m0+C
m0+C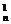 m1+…+C
m1+…+C mn,
mn,
(1+n)m=C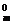 n0+C
n0+C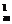 n1+…+C
n1+…+C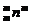 ,
,
又因为C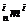 =
=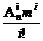 ,C
,C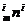 =
=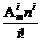 ,
,
而A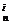 mi>A
mi>A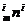 ,所以C
,所以C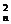 m2>C
m2>C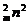 ,C
,C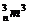 >C
>C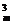 n3,…,C
n3,…,C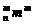 >C
>C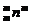 .
.
又因为C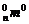 =C
=C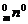 ,C
,C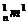 =C
=C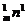 ,
,
所以(1+m)n>(1+n)m.
证法二:(1+m)n>(1+n)m
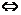 nln(1+m)>mln(1+n)
nln(1+m)>mln(1+n)
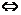
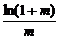 >
>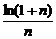 .
.
令f(x)=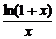 ,x∈[2,+∞],
,x∈[2,+∞],
只要证f(x)在[2,+∞]上单调递减,只要证f ′(x)<0.
f ′(x)=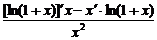 =
=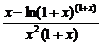 .
.
当x≥2时,x-lg(1+x)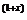 <0,
<0,
x2(1+x)>0,得f ′(x)<0,即x∈[2,+∞]时,f ′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
2.对于有附加条件的排列组合应用题,通常从三个途径考虑:
(1)以元素为主考虑,即先满足特殊元素的要求,再考虑其他元素.
(2)以位置为主考虑,即先满足特殊位置的要求,再考虑其他位置.
(3)先不考虑附加条件,计算出排列或组合数,再减去不合要求的排列或组合数.
1.对排列、组合的应用题应遵循两个原则:一是按元素的性质进行分类;二是按事件发生的过程进行分步.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com