
2.(2003年北京)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形.要使正方形与圆的面积之和最小,正方形的周长应为______________.
解析:设正方形周长为x,则圆的周长为1-x,半径r=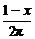 .
.
∴S正=(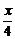 )2=
)2=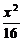 ,S圆=π·
,S圆=π·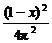 .
.
∴S正+S圆=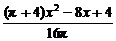 (0<x<1).
(0<x<1).
∴当x=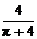 时有最小值.
时有最小值.
答案: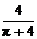
1.若奇函数f(x)在[a,b]上是增函数,且最小值是1,则f(x)在[-b,-a]上是
A.增函数且最小值是-1 B.增函数且最大值是-1
C.减函数且最小值是-1 D.减函数且最大值是-1
解析:f(a)=1,∴f(-a)=-1.
答案:B
5.函数y=|x-1|+|x-3|的最小值是______________.
解析:在数轴上,设1、3、x对应的点分别是A、B、P,∴y=|x-1|+|x-3|=|PA|+|PB|≥|AB|=2.
答案:2
●典例剖析
[例1] (2004年上海,18)某单位用木料制作如图所示的框架,框架的下部是边长分别为x、y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为8 m2,问x、y分别为多少时用料最省?(精确到0.001 m)

解:由题意得x·y+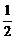 ·x·
·x·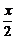 =8,
=8,
∴y=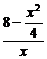 =
= -
-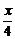 (0<x<4
(0<x<4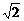 ).
).
于是,框架用料长度为
L=2x+2y+2(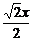 )=(
)=(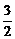 +
+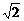 )x+
)x+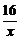 ≥2
≥2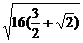 =4
=4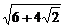 .
.
当且仅当(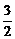 +
+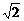 )x=
)x=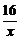 ,即x=
,即x=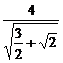 =8-4
=8-4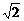 时,等号成立.
时,等号成立.
此时,x≈2.343,y=2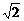 ≈2.828.
≈2.828.
故当x为2.343 m,y为2.828 m时,用料最省.
[例2] 设f(t)=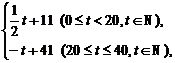
g(t)=-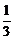 t+
t+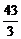 (0≤t≤40,t∈N*).
(0≤t≤40,t∈N*).
求S=f(t)g(t)的最大值.
解:当0≤t<20时,S=(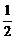 t+11)·(-
t+11)·(-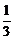 t+
t+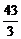 )=-
)=-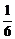 (t+22)(t-43).∵
(t+22)(t-43).∵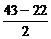 =10.5,又t∈N,∴t=10或11时,Smax=176.
=10.5,又t∈N,∴t=10或11时,Smax=176.
当20≤t≤40时,S=(-t+41)(-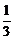 t+
t+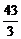 )=
)=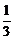 (t-41)(t-43).∴t=20时,Smax=161.
(t-41)(t-43).∴t=20时,Smax=161.
综上所述,S的最大值是176.
[例3] 设0<a<1,x和y满足logax+3logxa-logxy=3,如果y有最大值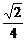 ,求这时a和x的值.
,求这时a和x的值.
解:原式可化为logax+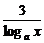 -
-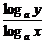 =3,即logay=loga2x-3logax+3=(logax-
=3,即logay=loga2x-3logax+3=(logax-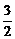 )2+
)2+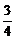 ,知当logax=
,知当logax=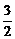 时,logay有最小值
时,logay有最小值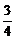 .
.
∵0<a<1,∴此时y有最大值a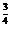 .
.
根据题意有a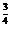 =
=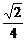
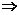 a=
a=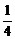 .这时x=a
.这时x=a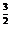 =(
=(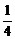 )
)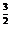 =
=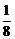 .
.
评述:本题是已知函数的最值,求函数式中的字母参数的值.这类问题,也是常见题型之一.
深化拓展
已知f(x)=2+log3x(1≤x≤9),求函数g(x)=[f(x)]2+f(x2)的最大值与最小值.
解:由f(x)的定义域为[1,9]可得g(x)的定义域为[1,3].
又g(x)=(2+log3x)2+(2+log3x2)=(log3x+3)2-3,
∵1≤x≤3,∴0≤log3x≤1.
∴当x=1时,g(x)有最小值6;
当x=3时,g(x)有最大值13.
答案:当x=1时,g(x)有最小值6;
当x=3时,g(x)有最大值13.
●闯关训练
夯实基础
4.设x>0,y>0且3x+2y=12,则xy的最大值是___________.
解析:∵x>0,y>0,
∴3x·2y≤(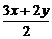 )2=62
)2=62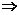 xy≤6(当且仅当3x=2y时等号成立).
xy≤6(当且仅当3x=2y时等号成立).
答案:6
3.(2004年春季安徽)函数y=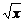 -x(x≥0)的最大值为___________________.
-x(x≥0)的最大值为___________________.
答案: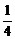
2.若x2+y2=1,则3x-4y的最大值为
A.3 B.4 C.5 D.6
解析:∵x2+y2=1,
∴可设x=cosα,y=sinα.
∴3x-4y=3cosα-4sinα=5sin(α+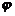 )≤5.
)≤5.
答案:C
1.(2003年春季北京)函数f(x)=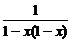 的最大值是
的最大值是
A.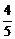 B.
B.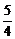 C.
C.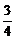 D.
D.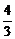
解析:∵1-x(1-x)=1-x+x2=(x-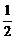 )2+
)2+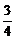 ≥
≥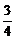 ,
,
∴f(x)=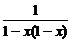 ≤
≤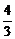 ,f(x)max=
,f(x)max=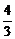 .
.
答案:D
2.10 函数的最值
●知识梳理
求函数最值的常用方法有:
(1)配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的最值;
(2)判别式法:若函数y=f(x)可以化成一个系数含有y的关于x的二次方程a(y)x2+ b(y)x+c(y)=0,则在a(y)≠0时,由于x、y为实数,故必须有Δ=b2(y)-4a(y)·
c(y)≥0,从而确定函数的最值,检验这个最值在定义域内有相应的x值.
(3)不等式法:利用平均值不等式取等号的条件确定函数的最值.
(4)换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.
(5)数形结合法:利用函数图象或几何方法求出函数的最值.
(6)函数的单调性法.
●点击双基
2.画分段函数的图象,求分段函数的定义域、值域是本节的一个难点.教学时,要指导学生按x的特点分好段,并向学生指明分段函数其实是一个函数,只是由于该函数在自变量取值的各个阶段其对应关系不一样才以分段式给出,因此它的定义域、值域应是各阶段相应集合的并集.
拓展题例
[例1] 设f(x)是定义在(-∞,+∞)上的函数,对一切x∈R均有f(x)+f(x+2)=0,当-1<x≤1时,f(x)=2x-1,求当1<x≤3时,函数f(x)的解析式.
解:设1<x≤3,则-1<x-2≤1,又对任意的x,有f(x)+f(x+2)=0,∴f(x+2)=-f(x).∴f(x-2)=-f[(x-2)+2]=-f(x).又-1<x-2≤1时,f(x-2)=2(x-2)-1=2x-5,∴f(x)=-f(x-2)=-2x+5(1<x≤3).
评述:将1<x≤3转化成-1<x-2≤1,再利用已知条件是解本题的关键.
[例2] 设m=(log2x)2+(t-2)log2x+1-t,若t在区间[-2,2]上变化时,m值恒正,求x的取值范围.
解:由m=[log2x+(t-1)](log2x-1)>0,得
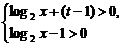 ①
①
或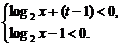 ②
②
在①中,(log2x-1)+t>0对于t∈[-2,2]恒成立时,应有log2x-1>2,即x>8;
在②中,(log2x-1)+t<0对于t∈[-2,2]恒成立时,应有log2x-1<-2,即0<
x<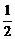 .
.
综上,得x>8或0<x<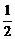 .
.
评述:本题还可用如下方法求解:m=(log2x-1)t+[(log2x)2-2log2x+1]关于变量t的图象是直线,要t∈[-2,2]时m值恒正,只要t=-2和2时m的值恒正,即有
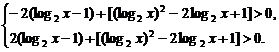
∴log2x>3或log2x<-1.
∴x>8或0<x<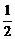 .
.
1.复习本节时,教师应先指导学生看课本,并对课本上的重要知识点归纳总结,对课本上的典型例题、典型习题要让学生再做,并注重一题多解、一题多变.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com