
1.函数f(x)在点x0处连续与f(x)在点x 0处有极限的联系与区别:
其联系是:f(x)在点x0处连续是依据f(x)在点x0处的极限来定义的,它要求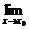 f(x)存在.
f(x)存在.
其区别是:函数在某点处连续比在此点处有极限所具备的条件更强.首先,f(x)在点x0处有极限,对于点x0而言,x0可以属于f(x)的定义域,也可以不属于f(x)的定义域,即与f(x0)是否有意义无关,而f(x)在点x0处连续,要求f(x)在点x0及其附近都有定义;其次,f(x)在点x0处的极限(值)与f(x)在点x0处的函数值f(x0)可以无关,而f(x)在点x0处连续,要求f(x)在点x0处的极限(值)等于它在这一点的函数值f(x0).我们通常说“连续必有极限,有极限未必连续”,正是针对上述事实而言的.
1.函数f(x)在点x0处连续反映到函数f(x)的图象上是在点x=x0处是不间断的.一般地,函数f(x)在点x0处不连续(间断)大致有以下几种情况(如下图所示).

图甲表示的是f(x)在点x0处的左、右极限存在但不相等,即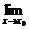 f(x)不存在.
f(x)不存在.
图乙表示的是f(x)在点x0处的左极限存在,而右极限不存在,也属于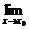 f(x)不存在的情况.
f(x)不存在的情况.
图丙表示的是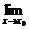 f(x)存在,但函数f(x)在点x0处没有定义.
f(x)存在,但函数f(x)在点x0处没有定义.
图丁表示的是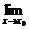 f(x)存在,但它不等于函数在这一点处的函数值f(x0).
f(x)存在,但它不等于函数在这一点处的函数值f(x0).
●教师下载中心
教学点睛
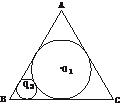
8.(2003年北京)如图,在边长为l的等边△ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切,…,圆On+1与圆On外切,且与AB、BC相切,如此无限继续下去,记圆On的面积为an(n∈N*).
(1)证明{an}是等比数列;
(2)求 (a1+a2+…+an)的值.
(a1+a2+…+an)的值.
(1)证明:记rn为圆On的半径,
则r1=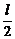 tan30°=
tan30°=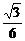 l.
l.
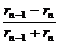 =sin30°=
=sin30°=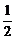 ,∴rn=
,∴rn=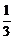 rn-1(n≥2).
rn-1(n≥2).
于是a1=πr12=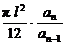 ,
,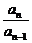 =(
=( )2=
)2=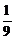 ,
,
∴{an}成等比数列.
(2)解:因为an=(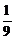 )n-1·a1(n∈N*),
)n-1·a1(n∈N*),
所以 (a1+a2+…+an)=
(a1+a2+…+an)=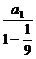 =
=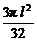 .
.
●思悟小结
7.(2002年春季上海)某公司全年的纯利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第1位职工得奖金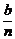 元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设ak(1≤k≤n)为第k位职工所得奖金额,试求a2、a3,并用k、n和b表示ak(不必证明);
(2)证明:ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b).对常数b,当n变化时,求 Pn(b)(可用公式
Pn(b)(可用公式 (1-
(1-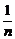 )n=
)n=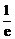 ).
).
(1)解:a1=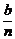 ,a2=
,a2=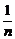 (1-
(1-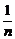 )·b,a3=
)·b,a3=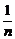 (1-
(1-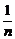 )2·b,…,ak=
)2·b,…,ak=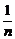 (1-
(1-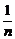 )k-1·b.
)k-1·b.
(2)证明:ak-ak+1=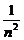 (1-
(1-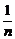 )k-1·b>0,此奖金分配方案体现了按劳分配的原则.
)k-1·b>0,此奖金分配方案体现了按劳分配的原则.
(3)解:设fk(b)表示发给第k位职工后所剩余额,则f1(b)=(1-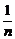 )·b,f2(b)=(1-
)·b,f2(b)=(1-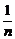 )2·b,…,f k(b)=(1-
)2·b,…,f k(b)=(1-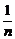 )k·b,
)k·b,
得Pn(b)=fn(b)=(1-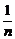 )n·b,
)n·b,
故 Pn(b)=
Pn(b)=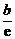 .
.
 探究创新
探究创新
6.求y=f(x)=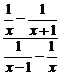 的不连续点.
的不连续点.
解:易求f(x)的定义域为{x|x≠-1,0,1},所以f(x)的不连续点为x=-1,x=0和x=1.
5.抛物线y=b(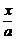 )2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以
)2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以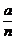 为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.
为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.
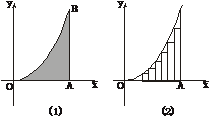
解:S= [b·(
[b·(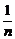 )2+b·(
)2+b·(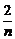 )2+b·(
)2+b·(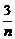 )2+…+b·(
)2+…+b·(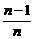 )2]2·
)2]2·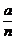
=
 ·ab
·ab
=
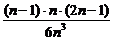 ·ab=
·ab=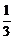 ab.
ab.
培养能力
4.有以下四个命题:
①f(x)=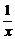 在[0,1]上连续;
在[0,1]上连续;
②若f(x)是(a,b)内的连续函数,则f(x)在(a,b)内有最大值和最小值;
③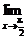
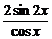 =4;
=4;
④若f(x)=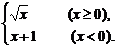 则
则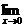 f(x)=0.
f(x)=0.
其中正确命题的序号是____________.(请把你认为正确命题的序号都填上)
答案:③
3.已知函数f(x)=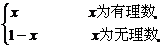 函数f(x)在哪点连续
函数f(x)在哪点连续
A.处处连续 B.x=1
C.x=0
D.x=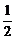
解析: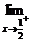 f(x)=
f(x)= 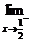 f(x)=f(
f(x)=f(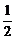 ).
).
答案:D
2.若f(x)在定义域[a,b]上有定义,则在该区间上
A.一定连续
B.一定不连续
C.可能连续也可能不连续
D.以上均不正确
解析:有定义不一定连续.
答案:C
1.函数f(x)=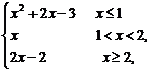 则有
则有
A.f(x)在x=1处不连续
B.f(x)在x=2处不连续
C.f(x)在x=1和x=2处不连续
D.f(x)处处连续
解析: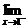 f(x)=0,
f(x)=0, 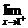 f(x)=1,
f(x)=1,
∴f(x)在x=1处不连续.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com