
8.已知函数f(x)=ln(ex+a)(a>0).
(1)求函数y=f(x)的反函数y=f-1(x)及f(x)的导数f′(x);
(2)假设对任意x∈[ln(3a),ln(4a)],不等式|m-f-1(x)|+ln(f′(x))<0成立,求实数m的取值范围.
解:(1)由y=f(x)=ln(ex+a),
得x=ln(ey-a),所以
y=f-1(x)=ln(e x-a)(x>lna).
f′(x)=[ln(ex+a)]′=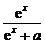 .
.
(2)由|m-f-1(x)|+ln(f′(x))<0,得
ln(ex-a)-ln(ex+a)+x<m<ln(ex-a)+ln(ex+a)-x.
设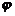 (x)=ln(ex-a)-ln(ex+a)+x,
(x)=ln(ex-a)-ln(ex+a)+x,
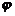 (x)=ln(ex-a)+ln(ex+a)-x,于是原不等式对于x∈[ln(3n),ln(4a)]恒成立.等价于
(x)=ln(ex-a)+ln(ex+a)-x,于是原不等式对于x∈[ln(3n),ln(4a)]恒成立.等价于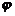 (x)<m<
(x)<m<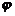 (x).
(*)
(x).
(*)
由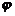 ′(x)=
′(x)=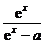 -
-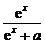 +1,
+1,
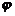 ′(x)=
′(x)= 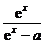 +
+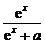 -1,注意到0<ex-a<ex<ex+a.
-1,注意到0<ex-a<ex<ex+a.
故有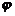 ′(x)>0,
′(x)>0, 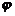 ′(x)>0,从而
′(x)>0,从而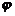 (x)、
(x)、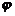 (x)均在[ln(3a),ln(4a)]上单调递增,因此不等式(*)成立当且仅当
(x)均在[ln(3a),ln(4a)]上单调递增,因此不等式(*)成立当且仅当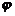 (ln(4a))<m<
(ln(4a))<m<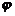 (ln(3a)),即ln(
(ln(3a)),即ln(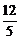 a)<m<ln(
a)<m<ln(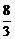 a).
a).
探究创新
7.已知函数f(x)=e-x(cosx+sinx),将满足f′(x)=0的所有正数x从小到大排成数列{xn}.
求证:数列{f(xn)}为等比数列.
证明:f′(x)=-e-x(cosx+sinx)+e-x(-sinx+cosx)=-2e-xsinx,
由f′(x)=0,即-2e-xsinx=0,
解得x=nπ,n∈Z.从而xn=nπ(n=1,2,3…),f(xn)=(-1)ne-πn.
所以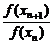 =-e-π.
=-e-π.
所以数列{f(xn)}是公比q=-e-π的等比数列.
6.设函数y=ax3+bx2+cx+d的图象与y轴交点为P点,且曲线在P点处的切线方程为12x-y-4=0.若函数在x=2处取得极值0,试确定函数的解析式.
解:∵y=ax3+bx2+cx+d的图象与y轴的交点为P,∴P的坐标为P(0,d).又曲线在点P处的切线方程为y=12x-4,P点坐标适合方程,从而d=-4.
又切线斜率k=12,故在x=0处的导数y′|x=0=12,而y′=3ax2+2bx+c,y′|x=0=c,从而 c=12.
又函数在x=2处取得极值0,所以
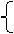 y′|x=2=0,
y′|x=2=0,
f(2)=0,即
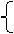 12a+4b+12=0,
12a+4b+12=0,
8a+4b+20=0.
解得a=2,b=-9.
∴所求函数解析式为y=2x3-9x2+12x-4.
培养能力
5.设f(x)在x=1处连续,且f(1)=0,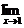
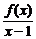 =2,求f′(1).
=2,求f′(1).
解:∵f(1)=0,
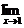
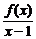 =2,
=2,
∴f′(1)= 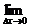
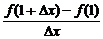
=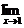
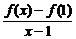 =
=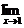
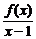 =2.
=2.
4.(2004年重庆,理14)曲线y=2-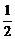 x2与y=
x2与y=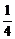 x3-2在交点处的切线夹角是__________.(以弧度数作答)
x3-2在交点处的切线夹角是__________.(以弧度数作答)
解析:由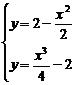 得x3+2x2-16=0,(x-2)(x2+4x+8)=0,∴x=2.
得x3+2x2-16=0,(x-2)(x2+4x+8)=0,∴x=2.
∴两曲线只有一个交点.
∵y′=(2-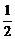 x2)′=-x,∴y′|x=2=-2.
x2)′=-x,∴y′|x=2=-2.
又y′=(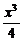 -2)′=
-2)′=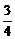 x2,∴当x=2时,y′=3.
x2,∴当x=2时,y′=3.
∴两曲线在交点处的切线斜率分别为-2、3,
|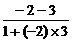 |=1.∴夹角为
|=1.∴夹角为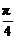 .
.
答案: 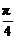
3.(2004年湖北,文3)已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为
A.f(x)=(x-1)2+3(x-1)
B.f(x)=2(x-1)
C.f(x)=2(x-1)2
D.f(x)=x-1
答案:A
2.(2004年全国Ⅳ,文4)函数y=(x+1)2(x-1)在x=1处的导数等于
A.1 B.2 C.3 D.4
解析:y′|x=1=[(x2+2x+1)(x-1)]′|x=1=[x3+x2-x-1]′|xx=1=(3x2+2x-1)| x=1=4.
答案:D
1.(2004年全国Ⅱ,文3)曲线y=x3-3x2+1在点(1,-1)处的切线方程为
A.y=3x-4 B.y=-3x+2
C.y=-4x+3 D.y=4x-5
解析:y′=3x2-6x,∴y′|x=1=-3.
∴在(1,-1)处的切线方程为y+1=-3(x-1).
答案:B
4.函数y=x2的曲线上点A处的切线与直线3x-y+1=0的夹角为45°,则点A的坐标为___________.
解析:设点A的坐标为(x0,y0),
则y′|x=x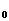 =2x|x=x
=2x|x=x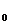 =2x
=2x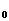 =k1,又直线3x-y+1=0的斜率k2=3.
=k1,又直线3x-y+1=0的斜率k2=3.
∴tan45°=1=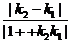 =|
=|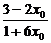 |.解得x0=
|.解得x0=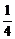 或x0=-1.∴y0=
或x0=-1.∴y0=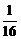 或y0=1,即A点坐标为(
或y0=1,即A点坐标为(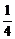 ,
,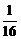 )或(-1,1).
)或(-1,1).
答案:(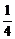 ,
,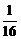 )或(-1,1)
)或(-1,1)
●典例剖析
[例1] 若f′(x0)=2,求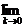
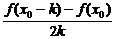 .
.
剖析:根据导数的定义.
解:f′(x0)= 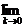
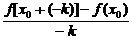 (这时Δx=-k).
(这时Δx=-k).
∴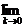
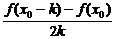
=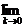 [-
[-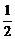 ·
·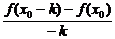 ]
]
=-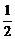 ·
·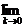
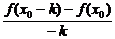
=-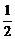 f′(x0)=-1.
f′(x0)=-1.
评述:注意f′(x0)=
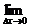
 中Δx的形式的变化,在上述变化中可以看到Δx=-k,k→0
中Δx的形式的变化,在上述变化中可以看到Δx=-k,k→0 -k→0,
-k→0,
∴f′(x0)= 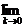
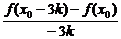 ,还可以写成f′(x0)=
,还可以写成f′(x0)=
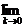
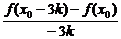 或 f′(x0)=
或 f′(x0)=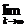 [f(x0+
[f(x0+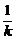 )-f(x0)]等.
)-f(x0)]等.
[例2] 若f(x)在R上可导,(1)求f(-x)在x=a处的导数与f(x)在x=-a处的导数的关系;(2)证明:若f(x)为偶函数,则f′(x)为奇函数.
剖析:(1)需求f(-x)在x=a处的导数与f(x)在x=-a处的导数;(2)求f′(x),然后判断其奇偶性.
(1)解:设f(-x)=g(x),则
g′(a)=
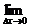

=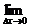
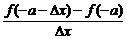
=-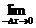
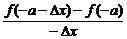
=-f′(-a).
∴f(-x)在x=a处的导数与f(x)在x=-a处的导数互为相反数.
(2)证明:f′(-x)=
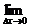
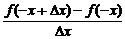
=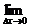
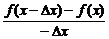
=-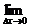
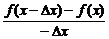
=-f′(x).
∴f′(x)为奇函数.
评述:用导数的定义求导数时,要注意Δy中自变量的变化量应与Δx一致.
深化拓展
(2)中若f(x)为奇函数,f′(x)的奇偶性如何?
[例3] 求下列函数的导数:
(1)y=x2sinx;
(2)y=ln(x+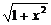 );
);
(3)y=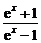 ;
;
(4)y=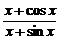 .
.
解:(1)y′=(x2)′sinx+x2(sinx)′=2xsinx+x2cosx.
(2)y′=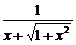 ·(x+
·(x+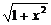 )′
)′
=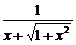 (1+
(1+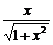 )
)
=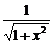 .
.
(3)y′=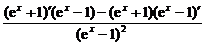
=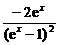 .
.
(4)y′=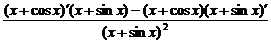
=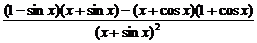
=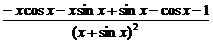 .
.
思考讨论
函数f(x)在点x0处是否可导与是否连续有什么关系?
●闯关训练
夯实基础
3.设f(x)=ax3+3x2+2,若f′(-1)=4,则a的值等于
A.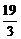 B.
B.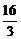 C.
C.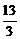 D.
D.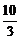
解析:f′(x)=3ax2+6x,f′(-1)=3a-6=4,所以a=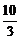 .
.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com