
1.常用的抽样方法有三种:简单随机抽样、系统抽样、分层抽样,其中第一种是最简单、最基本的抽样方法.三种抽样方法的共同点:都是等概率抽样,体现了抽样的公平性;三种抽样方法各有其特点和适用的范围.
2.用样本估计总体,是研究统计问题的一个基本思想方法.用样本估计总体,本节主要研究在整体上用样本的频率分布估计总体的分布.
●教师下载中心
教学点睛
1.采用什么抽样方法,要视情况来定:
当总体中的个体较少时,一般可用随机抽样;当总体中的个体较多时,一般可用系统抽样;当总体由差异明显的几部分组成时,一般可用分层抽样.
9.有点难度哟!
1936年,美国进行总统选举,竞选的是民主党的罗斯福和共和党的兰登,罗斯福是在任的总统.
美国权威的《文学摘要》杂志社,为了预测总统候选人谁能当选,采用了大规模的模拟选举,他们以电话簿上的地址和俱乐部成员名单上的地址发出1000万封信,收到回信200万封,在调查史上,样本容量这么大是少见的,杂志社花费了大量的人力和物力,他们相信自己的调查统计结果,即兰登将以57%对43%的比例获胜,并大力进行宣传.
最后选举结果却是罗斯福以62%对38%的巨大优势获胜,连任总统.这个调查使《文学摘要》杂志社威信扫地,不久只得关门停刊.试分析这次调查失败的原因.
解:失败的原因:抽样方法不正确.样本不是从总体(全体美国公民)中随机地抽取,1936年,美国有私人电话和参加俱乐部的家庭,都是比较富裕的家庭.1929-1933年的世界经济危机,使美国经济遭到沉重打击,“罗斯福新政”动用行政手段干预市场经济,损害了部分富人的利益,但广大的美国人民却从中得到了好处.所以,从这部分富人中抽取的样本严重偏离了总体,导致样本不具有代表性.
●思悟小结
8.有点难度哟!
从一个养鱼池中捕得m条鱼,作上记号后再放入池中,数日后又捕得n条鱼,其中k条有记号,请估计池中有多少条鱼.
解:设池中有N条鱼,第一次捕得m条作上记号后放入水池中,则池中有记号的鱼占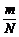 ;第二次捕得n条,则这n条鱼是一个样本,其中有记号的鱼占
;第二次捕得n条,则这n条鱼是一个样本,其中有记号的鱼占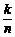 .我们用样本来估计总体分布,令
.我们用样本来估计总体分布,令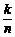 =
=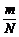 ,∴N=
,∴N=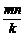 .
.
探究创新
7.有点难度哟!
某县政府机关在编人员100人,其中副处级以上干部10人,一般干部70人,工人20人,上级人事部门为了了解职工对机构改革的意见,要从中抽取一个容量为20的样本,试说明具体实施办法,并证明用这种抽样方法可使总体中每个个体被抽到的概率相等.
解:因机构改革关系到所有人的利益,故采用分层抽样方法较宜.
∵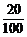 =
=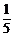 ,∴10×
,∴10×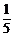 =2,70×
=2,70×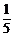 =14,20×
=14,20×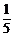 =4.
=4.
故从副处级以上干部中抽取2人,从一般干部中抽取14人,从工人中抽取4人.副处级以上干部被抽到的概率为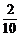 =
=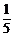 ,一般干部被抽到的概率为
,一般干部被抽到的概率为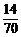 =
=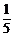 ,工人被抽到的概率为
,工人被抽到的概率为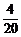 =
=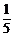 ,即每个个体被抽到的概率都是
,即每个个体被抽到的概率都是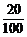 =
=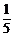 .
.
6.某工厂生产的产品,可分为一等品、二等品、三等品三类,根据抽样检验的记录有一等品54个、二等品140个、三等品6个.
(1)估计三种产品的概率;
(2)画出频率分布条形图.
解:(1)0.27,0.7,0.03.
(2)频率分布条形图如下.

5.举例说明简单随机抽样和分层抽样两种抽样方法,无论使用哪一种抽样方法,总体中的每一个个体被抽到的概率都相等.
解:袋中有160个小球,其中红球48个,蓝球64个,白球16个,黄球32个,从中抽取20个作为一个样本.
(1)使用简单随机抽样:每个个体被抽到的概率为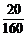 =
=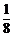 .
.
(2)使用分层抽样:四种球的个数比为3∶4∶1∶2.红球应抽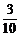 ×20=6个;蓝球应抽
×20=6个;蓝球应抽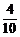 ×20=8个;白球应抽
×20=8个;白球应抽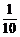 ×20=2个;黄球应抽
×20=2个;黄球应抽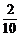 ×20=4个.由于
×20=4个.由于 =
= =
=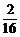 =
=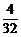 =
=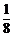 ,所以,按颜色区分,每个球被抽到的概率也都是
,所以,按颜色区分,每个球被抽到的概率也都是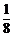 .
.
培养能力
4.下图是容量为100的样本的频率分布直方图,试根据图形中的数据填空:
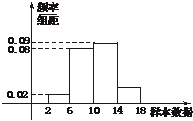
(1)样本数据落在范围[6,10)内的频率为___________;
(2)样本数据落在范围[10,14)内的频数为___________;
(3)总体在范围[2,6)内的概率约为___________.
答案:(1)0.32 (2)36 (3)0.08
3.某单位共有N个职工,要从N个职工中采用分层抽样法抽取n个样本,已知该单位的某一部门有M个员工,那么从这一部门中抽取的职工数为___________.
答案: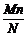
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com