1.若函数f(x)有导数，它的极值可在方程(x)=0的根处来考查，求函数y=f(x)的极值方法如下：

(1)求导数(x)；

(2)求方程(x)=0的根；

(3)检查(x)在方程(x)=0的根的左右的值的符号，如果左负右正，那么函数y=f(x)在这个根处取得极小值；如果左正右负，那么函数y=f(x)在这个根处取得极大值.

13.3　 导数的综合问题

●知识梳理

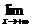
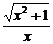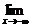
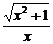3.在求函数极限时，需观察，对不能直接求的可以化简后求，但提醒学生要注意类似于与的区别.

拓展题例

[例1] 设f(x)=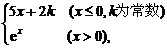问k为何值时，有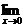f(x)存在？

解: 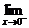f(x)=2k, 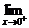f(x)=1,

∴要使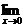f(x)存在，应有2k=1.∴k=.

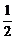[例2] a为常数，若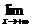(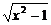－ax)=0,求a的值.

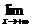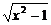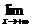
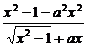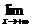
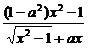解:∵(－ax)= ==0,

∴1－a²=0.

∴a=±1.但a=－1时，分母→0,

∴a=1.

2.函数极限比数列极限复杂之处在于它有左、右极限，并有趋近于无穷大和趋近于常数两类，需给予关注.

1.在讲解过程中，要讲清函数极限与数列极限的联系与区别，借助于函数图象讲清连续性的意义.

3.会熟练应用常见技巧求一些函数的极限.

●教师下载中心

教学点睛

2.函数f(x)在x₀处连续当且仅当满足三个条件：

(1)函数f(x)在x=x₀处及其附近有定义；

(2)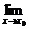f(x)存在；

(3) 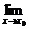f(x)=f(x₀).

1. 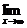f(x)=A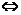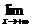f(x)= 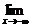f(x)=A,

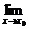f(x)=A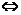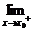f(x)=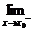f(x)=A.

9.设f(x)是x的三次多项式，已知

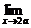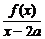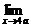
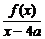===1.

试求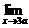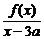的值(a为非零常数).

解:由于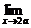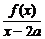=1,可知f(2a)=0.　　　 　　　　　　　　　　　　　　　　　①

同理f(4a)=0.　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　②

由①②，可知f(x)必含有(x－2a)与(x－4a)的因式，由于f(x)是x的三次多项式，故可设f(x)=A(x－2a)(x－4a)(x－C).

这里A、C均为待定的常数.

由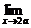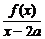=1,即

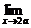
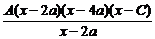
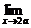=A(x－4a)(x－C)=1,

得A(2a－4a)(2a－C)=1,

即4a²A－2aCA=－1.　　　　　　 　　　　　　　　　　　　　　　　　　　　　　③

同理，由于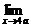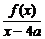=1,

得A(4a－2a)(4a－C)=1,

即8a²A－2aCA=1.　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　④

由③④得C=3a,A=,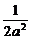

因而f(x)=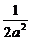(x－2a)(x－4a)(x－3a).

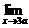
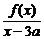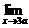
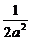∴=(x－2a)(x－4a)

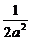=·a·(－a)=－.

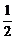●思悟小结

8.当a＞0时,求.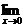

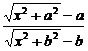解:原式=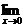

　=

==

=

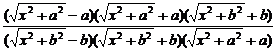
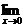
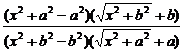
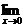
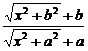探究创新