
3.下列四个命题中正确的是
A.若 an2=A2,则
an2=A2,则 an=A
an=A
B.若an>0, an=A,则A>0
an=A,则A>0
C.若 an=A,则
an=A,则 an2=A2
an2=A2
D.若 (an-b)=0,则
(an-b)=0,则 an=
an= bn
bn
解析:排除法,取an=(-1)n,排除A;
取an=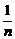 ,排除B;取an=bn=n,排除D.
,排除B;取an=bn=n,排除D.
答案:C
2.  [n(1-
[n(1-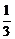 )(1-
)(1-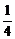 )(1-
)(1-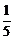 )…(1-
)…(1-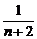 )]等于
)]等于
A.0 B.1 C.2 D.3
解析:  [n(1-
[n(1-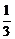 )(1-
)(1-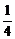 )(1-
)(1-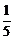 )…(1-
)…(1-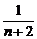 )]
)]
= [n×
[n×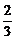 ×
×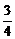 ×
×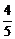 ×…×
×…×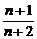 ]
]
=
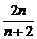 =2.
=2.
答案:C
1.下列极限正确的个数是
①
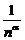 =0(α>0) ②
=0(α>0) ② qn=0
qn=0
③
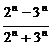 =-1 ④
=-1 ④ C=C(C为常数)
C=C(C为常数)
A.2 B.3
C.4 D.都不正确
解析:①③④正确.
答案:B
3.数列极限的四则运算法则:设数列{an}、{bn},
当 an=a,
an=a,  bn=b时,
bn=b时, (an±bn)=a±b;
(an±bn)=a±b;
 (an·bn)=a·b;
(an·bn)=a·b; 
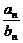 =
=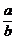 (b≠0).
(b≠0).
特别提示
(1)an、bn的极限都存在时才能用四则运算法则;
(2)可推广到有限多个.
●点击双基
2.几个常用的极限:① C=C(C为常数);②
C=C(C为常数);②
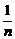 =0;③
=0;③ qn=0(|q|<1).
qn=0(|q|<1).
1.数列极限的定义:一般地,如果当项数n无限增大时,无穷数列{an}的项an无限地趋近于某个常数a(即|an-a|无限地接近于0),那么就说数列{an}以a为极限.
注:a不一定是{an}中的项.
13.2 数列的极限
●知识梳理
4.直线与曲线相切,并不一定只有一个公共点,当曲线是二次曲线时,由解析几何知,直线与曲线相切,有且只有一个公共点,即切点.
拓展题例
[例题] 曲线y=x2+1上过点P的切线与曲线y=-2x2-1相切,求点P的坐标.
解:设P(x0,y0),由题意知曲线y=x2+1在P点的切线斜率为k=2x0,切线方程为y=2x0x+1-x02,而此直线与曲线y=-2x2-1相切,
∴切线与曲线只有一个交点,即方程2x2+2x0x+2-x02=0的判别式
Δ=4x02-2×4×(2-x02)=0.
解得x0=±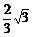 ,y0=
,y0=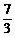 .
.
∴P点的坐标为(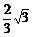 ,
,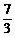 )或(-
)或(-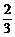
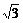 ,
,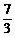 ).
).
3.若质点的运动规律为s=s(t),则质点在t=t0时的瞬时速度为v=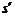 (t0).这就是导数的物理意义.
(t0).这就是导数的物理意义.
2.曲线C:y=f(x)在其上一点P(x0,f(x0))处的切线方程为
y-f(x0)=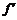 (x0)(x-x0).
(x0)(x-x0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com