
3.了解相互独立事件的意义,会用相互独立事件的概率乘法公式计算一些事件的概率,会计算事件在n次独立重复试验中恰好发生k次的概率.
●复习方略指南
概率是新课程中新增加部分的主要内容之一.这一内容是在学习排列、组合等计数知识之后学习的,主要内容为等可能性事件的概率、互斥事件有一个发生的概率及相互独立事件同时发生的概率.这一内容从2000年被列入新课程高考的考试说明.
在2000,2001,2002,2003,2004这五年高考中,新课程试卷每年都有一道概率解答题,并且这五年的命题趋势是:从分值上看,从10分提高到17分,从题目的位置看,2000年为第(17)题,2001年为第(18)题,2002年为第(19)题,2003年为第(20)题即题目的位置后移,2004年两题分值增加到17分.从概率在试卷中的分数比与课时比看,在试卷中的分数比(12∶150=1∶12.5)是在数学中课时比(约为11∶330=1∶30)的2.4倍.概率试题体现了考试中心提出的“突出应用能力考查”以及“突出新增加内容的教学价值和应用功能”的指导思想,在命题时,提高了分值,提高了难度,并设置了灵活的题目情境,如普法考试、串联并联系统、计算机上网、产品合格率等,所以在概率复习中要注意全面复习,加强基础,注重应用.
2.了解互斥事件的意义,会用互斥事件的概率加法公式计算一些事件的概率.
1.了解等可能性事件的概率的意义,会用排列组合公式计算一些等可能性事件的概率.
4.通项公式及其应用是二项式定理的基本问题,要熟练掌握.
拓展题例
[例题] 求(a-2b-3c)10的展开式中含a3b4c3项的系数.
解:(a-2b-3c)10=(a-2b-3c)(a-2b-3c)…(a-2b-3c),从10个括号中任取3个括号,从中取a;再从剩余7个括号中任取4个括号,从中取-2b;最后从剩余的3个括号中取-3c,得含a3b4c3的项为C a3C
a3C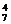 ·(-2b)4C
·(-2b)4C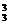 (-3c)3=C
(-3c)3=C C
C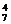 C
C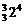 (-3)3a3b4c3.所以含a3b4c3项的系数为-C
(-3)3a3b4c3.所以含a3b4c3项的系数为-C C
C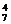 ×16×27.
×16×27.
3.要注意二项式定理在近似计算及证明整除性中的应用.
2.要注意区分项的系数与项的二项式系数.
1.要正确理解二项式定理,准确地写出二项式的展开式.
2.证明组合恒等式常用赋值法.
●教师下载中心
教学点睛
1.在使用通项公式T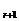 =C
=C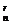
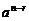 br时,要注意:
br时,要注意:
(1)通项公式是表示第r+1项,而不是第r项.
(2)展开式中第r+1项的二项式系数C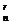 与第r+1项的系数不同.
与第r+1项的系数不同.
(3)通项公式中含有a,b,n,r,T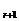 五个元素,只要知道其中的四个元素,就可以求出第五个元素.在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组).这里必须注意n是正整数,r是非负整数且r≤n.
五个元素,只要知道其中的四个元素,就可以求出第五个元素.在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组).这里必须注意n是正整数,r是非负整数且r≤n.
9.有点难度哟!
求证:2<(1+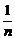 )n<3(n≥2,n∈N*).
)n<3(n≥2,n∈N*).
证明:(1+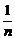 )n=C
)n=C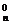 +C
+C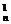 ×
×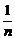 +C
+C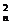 (
(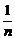 )2+…+C
)2+…+C (
(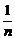 )n=1+1+C
)n=1+1+C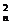 ×
×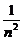 +C
+C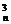 ×
×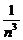 +…+C
+…+C ×
×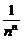 =2+
=2+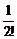 ×
×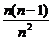 +
+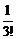 ×
×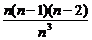 +…+
+…+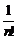 ×
×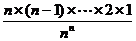 <2+
<2+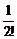 +
+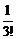
+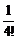 +…+
+…+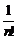 <2+
<2+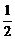 +
+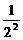 +
+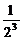 +…+
+…+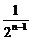 =2+
=2+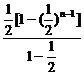 =3-(
=3-(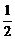 )
)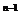 <3.显然(1+
<3.显然(1+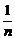 )n=1+1+C
)n=1+1+C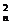 ×
×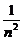 +C
+C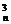 ×
×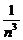 +…+C
+…+C ×
×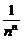 >2.所以2<(1+
>2.所以2<(1+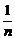 )n<3.
)n<3.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com