
4.体会数形结合、函数、方程思想在本章的运用.
●教师下载中心
教学点睛
3.注意极值与最值的关系,理解若只有一个极值则必为最值.
2.函数f(x)在极值点不一定可导,如函数y=|x|在x=0处.
1. (x0)=0是x0为可导函数f(x)的极值点的必要不充分条件,如函数y=x3在x=0处.
(x0)=0是x0为可导函数f(x)的极值点的必要不充分条件,如函数y=x3在x=0处.
10.有点难度哟!
(2000年全国)用总长14.8 m的钢条作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5 m,那么高为多少时容器的容积最大?并求出它的最大容积.
解:设容器底面短边长为x m,则另一边长为(x+0.5) m,高为
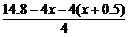 =3.2-2x(m).
=3.2-2x(m).
由3.2-2x>0和x>0得0<x<1.6.
设容器的容积为y m3,
则有y=x(x+0.5)(3.2-2x)(0<x<1.6),
整理,得y=-2x3+2.2x2+1.6x.
∴y′=-6x2+4.4x+1.6.
令y′=0,有-6x2+4.4x+1.6=0,即15x2-11x-4=0.
解得x1=1或x2=-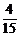 (不合题意,舍去).
(不合题意,舍去).
从而在定义域(0,1.6)内只有在x=1处使得y′=0.
因此,当x=1时,y取得最大值且ymax=-2+2.2+1.6=1.8,这时,高为3.2-2×1=1.2.
●思悟小结
9.已知f(x)=ax5-bx3+c(a>0)在x=±1处有极值,且极大值为4,极小值为0,试确定a、b、c的值.
解:已知f(x)=ax5-bx3+c,
所以 (x)=5ax4-3bx2=x2(5ax2-3b).
(x)=5ax4-3bx2=x2(5ax2-3b).
根据题意 (x)=0应有根x=±1,
(x)=0应有根x=±1,
故5a=3b.
所以 (x)=5ax2(x2-1).
(x)=5ax2(x2-1).
因a>0时,列表:
|
x |
(-∞,-1) |
-1 |
(-1,1) |
1 |
(1,+∞) |
 (x) (x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
 |
极大值 |
 ? ? |
极小值? |
 |
|
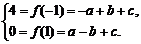
①+②得c=2,
①-②得b=a+2.
又5a=3b,所以a=3,b=5,c=2.
探究创新
8.已知实数a>0,函数f(x)=ax(x-2)2(x∈R)有极大值32.
(1)求实数a的值;
(2)求函数f(x)的单调区间.
解:(1)∵f(x)=ax(x-2)2=ax3-4ax2+4ax,
∴ (x)=3ax2-8ax+4a.
(x)=3ax2-8ax+4a.
由 (x)=0,得3ax2-8ax+4a=0.
(x)=0,得3ax2-8ax+4a=0.
∵a≠0,∴3x2-8x+4=0.
解得x=2或x=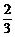 .
.
∵a>0,∴x<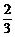 或x>2时,
或x>2时, (x)>0;
(x)>0;
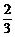 <x<2时,
<x<2时, (x)<0.
(x)<0.
∴当x=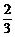 时,f(x)有极大值32,即
时,f(x)有极大值32,即
 a-
a-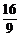 a+
a+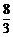 a=32,∴a=27.
a=32,∴a=27.
(2)f(x)在(-∞,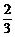 )和(2,+∞)上是增函数,在(
)和(2,+∞)上是增函数,在(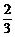 ,2)上是减函数.
,2)上是减函数.
7.已知函数f(x)=4x3+ax2+bx+5的图象在x=1处的切线方程为y=-12x.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-3,1]上的最值.
解:(1) (x)=12x2+2ax+b,
(x)=12x2+2ax+b, (1)=12+2a+b=-12. ①
(1)=12+2a+b=-12. ①
又x=1,y=-12在f(x)的图象上,
∴4+a+b+5=-12. ②
由①②得a=-3,b=-18,
∴f(x)=4x3-3x2-18x+5.
(2) (x)=12x2-6x-18=0,得x=-1,
(x)=12x2-6x-18=0,得x=-1, 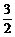 ,f(-1)=16,f(
,f(-1)=16,f(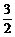 )=-
)=-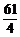 ,f(-3)=-76,f(1)=-13.
,f(-3)=-76,f(1)=-13.
∴f(x)的最大值为16,最小值为-76.
6.直线y=a与函数f(x)=x3-3x的图象有三个互不相同的公共点,求a的取值范围.
解:先求函数f(x)的单调区间,由 (x)=3x2-3=0,得x=±1.当x<-1或x>1时,
(x)=3x2-3=0,得x=±1.当x<-1或x>1时, (x)>0;当-1<x<1时,
(x)>0;当-1<x<1时, (x)<0.
(x)<0.
∴在(-∞,-1)和(1,+∞)上,f(x)=x3-3x是增函数;
在(-1,1)上,f(x)=x3-3x是减函数,由此可以作出f(x)=x3-3x的草图(如图).
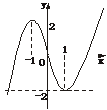
由图可知,当且仅当-2<a<2时,直线y=a与函数f(x)=x3-3x的图象有三个互不相同的公共点.
培养能力
5.如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
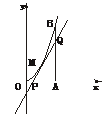
(1)试用t表示切线PQ的方程;
(2)试用t表示△QAP的面积g(t),若函数g(t)在[m,n]上单调递减,试求出m的最小值.
解:(1) (x)=2x,
(x)=2x,
∴k=2t,切线PQ的方程为
y-t2=2t(x-t),即2tx-y-t2=0.
(2)由(1)可求得P(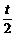 ,0),Q(6,12t-t2),
,0),Q(6,12t-t2),
∴g(t)=S△QAP=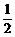 (6-
(6-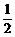 t)(12t-t2)=
t)(12t-t2)=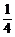 t3-6t2+36t(0<t<6),g′(t)=
t3-6t2+36t(0<t<6),g′(t)=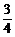 t2-12t+36.令g′(t)<0,得4<t<12.
t2-12t+36.令g′(t)<0,得4<t<12.
考虑到0<t<6,∴4<t<6,即g(t)的单调减区间为(4,6).
∴m的最小值为4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com