
5.自抛物线y2=2x上任意一点P向其准线l引垂线,垂足为Q,连结顶点O与P的直线和连结焦点F与Q的直线交于R点,求R点的轨迹方程.
解:设P(x1,y1)、R(x,y),则Q(-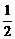 ,y1)、F(
,y1)、F(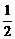 ,0),
,0),
∴OP的方程为y=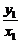 x, ①
x, ①
FQ的方程为y=-y1(x-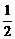 ). ②
). ②
由①②得x1=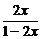 ,y1=
,y1=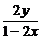 ,
,
代入y2=2x,可得y2=-2x2+x.
4.与圆x2+y2-4x=0外切,且与y轴相切的动圆圆心的轨迹方程是____________.
解析:若动圆在y轴右侧,则动圆圆心到定点(2,0)与到定直线x=-2的距离相等,其轨迹是抛物线;若动圆在y轴左侧,则动圆圆心轨迹是x负半轴.
答案:y2=8x(x>0)或y=0(x<0)
3.曲线x2+4y2=4关于点M(3,5)对称的曲线方程为____________.
解析:代入法(或相关点法).
答案:(x-6)2+4(y-10)2=4
2.(2003年河南)已知双曲线中心在原点且一个焦点为F(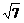 ,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-
,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-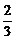 ,则此双曲线的方程是
,则此双曲线的方程是
A.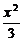 -
-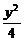 =1
B.
=1
B.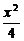 -
-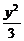 =1
=1
C.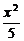 -
-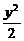 =1
D.
=1
D.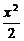 -
-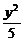 =1
=1
解析:设双曲线方程为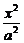 -
-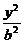 =1.
=1.
将y=x-1代入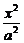 -
-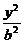 =1,
=1,
整理得(b2-a2)x2+2a2x-a2-a2b2=0.
由韦达定理得x1+x2=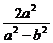 ,
,
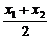 =
=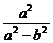 =-
=-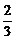 .
.
由c2=a2+b2求得a2=2,b2=5.
答案:D
1.已知M(-2,0)、N(2,0),|PM|-|PN|=4,则动点P的轨迹是
A.双曲线 B.双曲线左边一支
C.一条射线 D.双曲线右边一支
解析:利用几何性质.
答案:C
5.已知△ABC中,B(1,0)、C(5,0),点A在x轴上方移动,且tanB+tanC=3,则 △ABC的重心G的轨迹方程为________________.
解析:设A(x0,y0),
∵tanB+tanC=3,
∴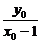 -
-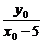 =3,点A的轨迹方程为y0=-
=3,点A的轨迹方程为y0=-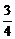 (x02-6x0+5)(x0≠1且x0≠5).若 G(x,y)为△ABC的重心,则由重心坐标公式:x=
(x02-6x0+5)(x0≠1且x0≠5).若 G(x,y)为△ABC的重心,则由重心坐标公式:x=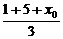 ,y=
,y=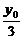 ,∴x0=3x-6,且y0=3y.代入A点轨迹方程得G的轨迹方程为y-1=-
,∴x0=3x-6,且y0=3y.代入A点轨迹方程得G的轨迹方程为y-1=-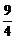 (x-3)2(x≠
(x-3)2(x≠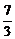 且x≠
且x≠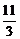 ).
).
答案:y-1=-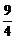 (x-3)2(x≠
(x-3)2(x≠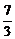 且x≠
且x≠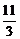 )
)
●典例剖析
[例1] 在△PMN中,tan∠PMN=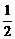 ,tan∠MNP=-2,且△PMN的面积为1,建立适当的坐标系,求以M、N为焦点,且过点P的椭圆的方程.
,tan∠MNP=-2,且△PMN的面积为1,建立适当的坐标系,求以M、N为焦点,且过点P的椭圆的方程.
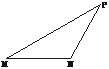
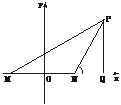
剖析:如上图,以直线MN为x轴,线段MN的垂直平分线为y轴,建立平面直角坐标系,则所求椭圆方程为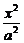 +
+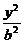 =1.显然a2、b2是未知数,但a2、b2与已知条件没有直接联系,因此应寻找与已知条件和谐统一的未知元,或改造已知条件.
=1.显然a2、b2是未知数,但a2、b2与已知条件没有直接联系,因此应寻找与已知条件和谐统一的未知元,或改造已知条件.
解法一:如上图,过P作PQ⊥MN,垂足为Q,
令|PQ|=m,于是可得|MQ|=|PQ|cot∠PMQ=2m,|QN|=|PQ|cot∠PNQ=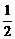 m.
m.
∴|MN|=|MQ|-|NQ|=2m-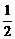 m=
m=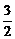 m.
m.
于是S△PMN=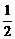 |MN|·|PQ|=
|MN|·|PQ|=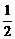 ·
·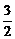 m·m=1.
m·m=1.
因而m=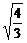 ,|MQ|=2
,|MQ|=2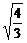 ,|NQ|=
,|NQ|=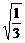 ,|MN|=
,|MN|=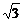 .
.
|MP|=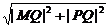 =
=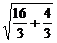 =
=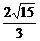 ,
,
|NP|=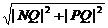 =
=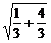 =
=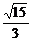 .
.
以MN的中点为原点,MN所在直线为x轴建立直角坐标系,设椭圆方程为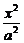 +
+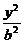 =1(a>b>0).
=1(a>b>0).
则2a=|MP|+|NP|=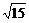 ,
,
2c=|MN|=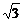 ,
,
故所求椭圆方程为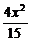 +
+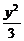 =1.
=1.
解法二:设M(-c,0)、N(c,0),P(x,y),y>0,
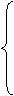
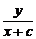 =
=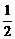 ,
,
|
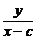 =2,
=2,
y·c=1,
解之,得x=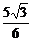 ,y=
,y=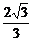 ,c=
,c=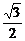 .
.
设椭圆方程为b2x2+a2y2=a2b2,则
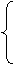 b2·(
b2·(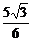 )2+a2(
)2+a2(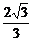 )2=a2b2,
)2=a2b2,
a2-b2=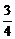 ,
,
解之,得a2=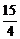 ,b2=3.
,b2=3.
(以下略)
评述:解法一选择了与a较接近的未知元|PM|、|PN|,但需改造已知条件,以便利用正弦定理和面积公式;解法二以条件为主,选择了与条件联系最直接的未知元x、y、c.本题解法较多,但最能体现方程思想方法的、学生易于理解和接受的是这两种解法.
深化拓展
若把△PMN的面积为1改为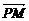 ·
·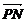 =
=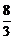 ,求椭圆方程.
,求椭圆方程.
提示:由tan∠PMN=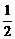 ,tan∠MNP=-2,
,tan∠MNP=-2,
易得sin∠MPN=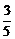 ,cos∠MPN=
,cos∠MPN=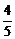 .
.
由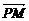 ·
·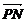 =
=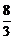 ,得|
,得|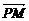 ||
||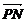 |=
|=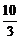 .
.
易求得|PM|=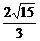 ,|PN|=
,|PN|=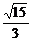 .
.
进而求得椭圆方程为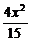 +
+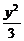 =1.
=1.
[例2] (2004年福建,22)如下图,P是抛物线C:y=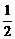 x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
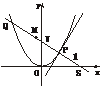
剖析:欲求PQ中点M的轨迹方程,需知P、Q的坐标.思路一,P、Q是直线l与抛物线C的交点,故需求直线l的方程,再与抛物线C的方程联立,利用韦达定理、中点坐标公式可求得M的轨迹方程;思路二,设出P、Q的坐标,利用P、Q的坐标满足抛物线C的方程,代入抛物线C的方程相减得PQ的斜率,利用PQ的斜率就是l的斜率,可求得M的轨迹方程.
解:设P(x1,y1)、Q(x2,y2)、M(x0,y0),依题意知x1≠0,y1>0,y2>0.
由y=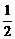 x2, ①
x2, ①
得y′=x.
∴过点P的切线的斜率k切=x1,
∴直线l的斜率kl=-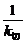 =-
=-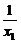 ,
,
直线l的方程为y-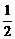 x12=-
x12=-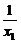 (x-x1). ②
(x-x1). ②
方法一:联立①②消去y,得x2+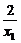 x-x12-2=0.
x-x12-2=0.
∵M为PQ的中点,
|
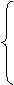 x0=
x0=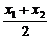 =-
=-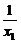 ,
,
y0=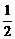 x12-
x12-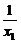 (x0-x1).
(x0-x1).
消去x1,得y0=x02+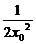 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+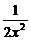 +1(x≠0).
+1(x≠0).
方法二:由y1=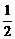 x12,y2=
x12,y2=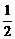 x22,x0=
x22,x0=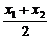 ,
,
得y1-y2=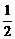 x12-
x12-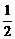 x22=
x22=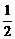 (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=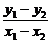 =kl=-
=kl=-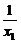 ,
,
∴x1=-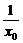 .
.
将上式代入②并整理,得y0=x02+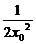 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+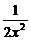 +1(x≠0).
+1(x≠0).
评述:本题主要考查了直线、抛物线的基础知识,以及求轨迹方程的常用方法.本题的关键是利用导数求切线的斜率以及灵活运用数学知识分析问题、解决问题.
深化拓展
当点P在抛物线C上移动时,求点M到x轴的最短距离.
提示:∵x≠0,x2>0,∴y=x2+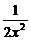 +1≥2
+1≥2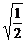 +1=
+1=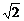 +1,当且仅当x2=
+1,当且仅当x2=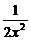 ,x=±
,x=±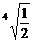 时等号成立,即点M到x轴的最短距离为
时等号成立,即点M到x轴的最短距离为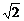 +1.
+1.
[例3] (2000年春季全国)已知抛物线y2=4px(p>0),O为顶点,A、B为抛物线上的两动点,且满足OA⊥OB,如果OM⊥AB于M点,求点M的轨迹方程.
剖析:点M是OM与AB的交点,点M随着A、B两点的变化而变化,而A、B为抛物线上的动点,点M与A、B的直接关系不明显,因此需引入参数.
解法一:设M(x0,y0),
则kOM=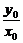 ,kAB=-
,kAB=-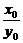 ,
,
直线AB方程是y=-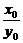 (x-x0)+y0.
(x-x0)+y0.
由y2=4px可得x=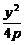 ,将其代入上式,整理,得
,将其代入上式,整理,得
x0y2-(4py0)y-4py02-4px02=0. ①
此方程的两根y1、y2分别是A、B两点的纵坐标,
∴A(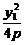 ,y1)、B(
,y1)、B(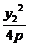 ,y2).
,y2).
∵OA⊥OB,∴kOA·kOB=-1.
∴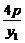 ·
·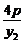 =-1.∴y1y2=-16p2.
=-1.∴y1y2=-16p2.
根据根与系数的关系,由①可得
y1·y2=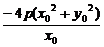 ,
,
∴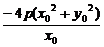 =16p2.
=16p2.
化简,得x02+y02-4px0=0,
即x2+y2-4px=0(除去原点)为所求.
∴点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法二:设A、B两点坐标为A(pt12,2pt1)、B(pt22,2pt2).
∴kOA=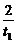 ,kOB=
,kOB=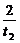 ,kAB=
,kAB=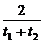 .
.
∵OA⊥OB,∴t1·t2=-4.
∴AB方程是y-2pt1=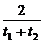 (x-pt12), ①
(x-pt12), ①
直线OM的方程是y=-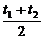 x. ②
x. ②
①×②,得(px)t12+2pyt1-(x2+y2)=0. ③
∴直线AB的方程还可写为
y-2pt2=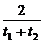 (x-pt22). ④
(x-pt22). ④
由②×④,得(px)t22+(2py)t2-(x2+y2)=0. ⑤
由③⑤可知t1、t2是方程(px)t2+(2py)t2-(x2+y2)=0的两根.
由根与系数的关系可得
t1t2=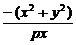 .又t1·t2=-4,
.又t1·t2=-4,
∴x2+y2-4px=0(原点除外)为所求点M的轨迹方程.
故M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法三:设M(x,y),直线AB方程为y=kx+b,
由OM⊥AB得k=-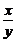 .
.
由y2=4px及y=kx+b消去y,得
k2x2+x(2kb-4p)+b2=0.
所以x1x2=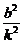 .消去x,得ky2-4py+4pb=0.
.消去x,得ky2-4py+4pb=0.
所以y1y2=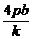 .由OA⊥OB,
.由OA⊥OB,
得y1y2=-x1x2,
所以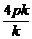 =-
=-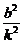 ,b=-4kp.
,b=-4kp.
故y=kx+b=k(x-4p).
用k=-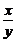 代入,得
代入,得
x2+y2-4px=0(x≠0).
解法四:设点M的坐标为(x,y),直线OA的方程为y=kx,
|
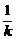 x.
x.
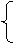
|
y2=4px,
类似地可得B点的坐标为(4pk2,-4pk),
从而知当k≠±1时,
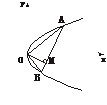
kAB=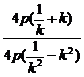
=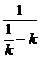 .
.
故得直线AB的方程为y+4pk=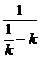 (x-4pk2),即(
(x-4pk2),即(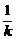 -k)y+4p=x,
①
-k)y+4p=x,
①
直线OM的方程为y=-(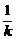 -k)x.
②
-k)x.
②
可知M点的坐标同时满足①②,
由①及②消去k便得4px=x2+y2,
即(x-2p)2+y2=4p2,但x≠0,
当k=±1时,容易验证M点的坐标仍适合上述方程.
故点M的轨迹方程为(x-2p)2+y2=4p2(x≠0),
它表示以点(2p,0)为圆心,以2p为半径的圆.
评述:本题考查了交轨法、参数法求轨迹方程,涉及了类比、分类讨论等数学方法,消参时又用到了整体思想法,对含字母的式子的运算能力有较高的要求,同时还需要注意轨迹的“完备性和纯粹性”.此题是综合考查学生能力的一道好题.
深化拓展
本题中直线AB恒过定点(4p,0),读者不妨探究一番.
●闯关训练
夯实基础
4.F1、F2为椭圆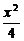 +
+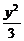 =1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,则点D的轨迹方程是________________.
=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,则点D的轨迹方程是________________.
解析:延长F1D与F2A交于B,连结DO,可知DO=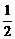 F2B=2,∴动点D的轨迹方程为x2+y2=4.
F2B=2,∴动点D的轨迹方程为x2+y2=4.
答案:x2+y2=4
3.已知A(0,7)、B(0,-7)、C(12,2),以C为一个焦点作过A、B的椭圆,椭圆的另一个焦点F的轨迹方程是
A.y2-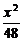 =1(y≤-1)
B.y2-
=1(y≤-1)
B.y2-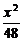 =1
=1
C.y2-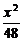 =-1 D.x2-
=-1 D.x2-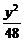 =1
=1
解析:由题意|AC|=13,|BC|=15,
|AB|=14,又|AF|+|AC|=|BF|+|BC|,
∴|AF|-|BF|=|BC|-|AC|=2.
故F点的轨迹是以A、B为焦点,实轴长为2的双曲线下支.又c=7,a=1,b2=48,
所以轨迹方程为y2-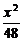 =1(y≤-1).
=1(y≤-1).
答案:A
2.(2005年春季北京,6)已知双曲线的两个焦点为F1(-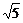 ,0)、F2(
,0)、F2(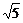 ,0),P是此双曲线上的一点,且PF1⊥PF2,|PF1|·|PF2|=2,则该双曲线的方程是
,0),P是此双曲线上的一点,且PF1⊥PF2,|PF1|·|PF2|=2,则该双曲线的方程是
A.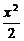 -
-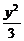 =1 B.
=1 B.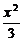 -
-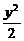 =1
=1
C.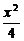 -y2=1
D.x2-
-y2=1
D.x2-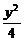 =1
=1
解析:设双曲线的方程为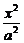 -
-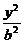 =1.
=1.
由题意||PF1|-|PF2||=2a,
|PF1|2+|PF2|2=(2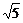 )2.
)2.
又∵|PF1|·|PF2|=2,
∴a=2,b=1.
故双曲线方程为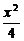 -y2=1.
-y2=1.
答案:C
1.动点P到直线x=1的距离与它到点A(4,0)的距离之比为2,则P点的轨迹是
A.中心在原点的椭圆
B.中心在(5,0)的椭圆
C.中心在原点的双曲线
D.中心在(5,0)的双曲线
解析:直接法.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com