
5.如下图,在杨辉三角中,从上往下数共有n(n∈N*)行,在这些数中非1的数字之和是___________________.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……
解析:观察可知,第n(n∈N*)行中有n个数,从左向右依次是二项式系数C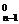 ,C
,C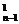 ,C
,C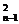 ,…,C
,…,C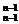 ,故当n≥3时,除了1外,第n行各数的和为an=C
,故当n≥3时,除了1外,第n行各数的和为an=C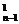 +C
+C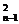 +…+C
+…+C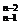 =2n-1-2.又前两行全部为数字1,故前n行非1的数字之和为a3+a4+…+an=
=2n-1-2.又前两行全部为数字1,故前n行非1的数字之和为a3+a4+…+an=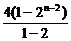 -2(n-2)=2n-2n.
-2(n-2)=2n-2n.
答案:2n-2n
●典例剖析
[例1] 已知等比数列{an}中,a1+a2+a3=7,a1a2a3=8,求an.
剖析:利用等比数列的基本量a1,q,根据条件求出a1和q.
解:设{an}的公比为q,由题意知
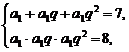
解得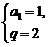 或
或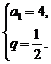 ∴an=2n-1或an=23-n.
∴an=2n-1或an=23-n.
评述:转化成基本量解方程是解决数列问题的基本方法.
思考讨论
用a2和q来表示其他的量好解吗?该题的{an}若成等差数列呢?
[例2] 已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:a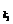 ,a
,a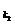 ,…,a
,…,a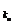 ,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
剖析:运用等差(比)数列的定义分别求得a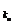 ,然后列方程求得kn.
,然后列方程求得kn.
解:设{an}的首项为a1,∵a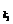 、a
、a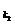 、a
、a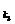 成等比数列,∴(a1+4d)2=a1(a1+16d).
成等比数列,∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=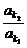 =3.
=3.
∵a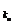 =a1+(kn-1)d,又a
=a1+(kn-1)d,又a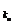 =a1·3n-1,
=a1·3n-1,
∴kn=2·3n-1-1.
∴k1+k2+…+kn=2(1+3+…+3n-1)-n
=2×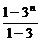 -n=3n-n-1.
-n=3n-n-1.
评述:运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:a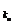 是等差数列中的第kn项,而是等比数列中的第n项.
是等差数列中的第kn项,而是等比数列中的第n项.
[例3] 设各项均为正数的数列{an}和{bn}满足5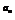 ,5
,5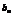 ,5
,5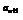 成等比数列,lgbn,lgan+1,lgbn+1成等差数列,且a1=1,b1=2,a2=3,求通项an、bn.
成等比数列,lgbn,lgan+1,lgbn+1成等差数列,且a1=1,b1=2,a2=3,求通项an、bn.
剖析:由等比中项、等差中项的性质得an+1=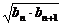 递推出an=
递推出an=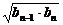 (n≥2).
(n≥2).
解:∵5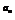 ,5
,5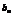 ,5
,5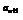 成等比数列,
成等比数列,
∴(5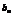 )2=5
)2=5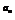 ·5
·5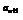 ,即2bn=an+an+1. ①
,即2bn=an+an+1. ①
又∵lgbn,lgan+1,lgbn+1成等差数列,
∴2lgan+1=lgbn+lgbn+1,即an+12=bn·bn+1. ②
由②及ai>0,bj>0(i、j∈N*)可得
an+1=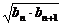 . ③
. ③
∴an=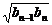 (n≥2). ④
(n≥2). ④
将③④代入①可得2bn=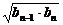 +
+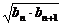 (n≥2),
(n≥2),
∴2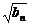 =
=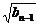 +
+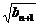 (n≥2).
(n≥2).
∴数列{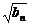 }为等差数列.
}为等差数列.
∵b1=2,a2=3,a22=b1·b2,∴b2=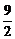 .
.
∴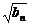 =
=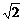 +(n-1)(
+(n-1)(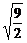 -
-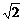 )
)
=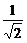 (n+1)(n=1也成立).
(n+1)(n=1也成立).
∴bn=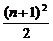 .
.
∴an=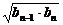 =
=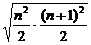
=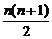 (n≥2).
(n≥2).
又当n=1时,a1=1也成立.
∴an=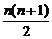 .
.
评述:由Sn求an时要注意验证a1与S1是否一致.
特别提示
4.(2004年全国,文14)已知等比数列{an}中,a3=3,a10=384,则该数列的通项an=___________________.
解析:由已知得q7=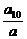 =128=27,故q=2.∴an=a3·qn-3=3·2n-3.
=128=27,故q=2.∴an=a3·qn-3=3·2n-3.
答案:3·2n-3
3.某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需过滤的次数为
A.5 B.10 C.14 D.15
解析:由题意列式(1-20%)n<5%,两边取对数得n>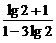 ≈13.4.故n≥14.
≈13.4.故n≥14.
答案:C
2.设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…·a30=230,那么a3·a6·a9·…·a30等于
A.210 B.220 C.216 D.215
解析:由等比数列的定义,a1·a2·a3=(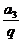 )3,故a1·a2·a3·…·a30=(
)3,故a1·a2·a3·…·a30=(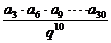 )3.又q=2,故a3·a6·a9·…·a30=220.
)3.又q=2,故a3·a6·a9·…·a30=220.
答案:B
1.一个直角三角形三内角的正弦值成等比数列,其最小内角是
A.arccos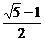 B.arcsin
B.arcsin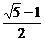
C.arccos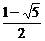 D.arcsin
D.arcsin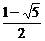
解析:设Rt△ABC中,C=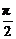 ,则A与B互余且A为最小内角.又由已知得sin2B=sinA,即cos2A=sinA,1-sin2A=sinA,解之得sinA=
,则A与B互余且A为最小内角.又由已知得sin2B=sinA,即cos2A=sinA,1-sin2A=sinA,解之得sinA=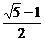 或sinA=
或sinA=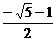 (舍).
(舍).
答案:B
6.证明等比数列的方法:(1)用定义:只需证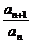 =常数;(2)用中项性质:只需an+12=an·an+2或
=常数;(2)用中项性质:只需an+12=an·an+2或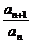 =
=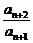 .
.
●点击双基
5.三个数或四个数成等比数列且又知积时,则三个数可设为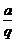 、a、aq,四个数可设为
、a、aq,四个数可设为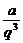 、
、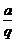 、aq、aq3为好.
、aq、aq3为好.
4.等比中项:若a、b、c成等比数列,则b为a、c的等比中项,且b=±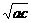 .
.
3.前n项和Sn=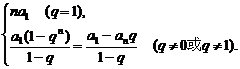
注:q≠1时,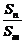 =
=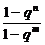 .
.
2.通项公式:an=a1qn-1,
推广形式:an=amqn-m.
变式:q=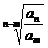 (n、m∈N*).
(n、m∈N*).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com