
1.过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有
A.1条 B.2条 C.3条 D.4条
解析:数形结合法,同时注意点在曲线上的情况.
答案:B
8.4 直线与圆锥曲线的位置关系
●知识梳理
本节主要内容是直线与圆锥曲线公共点问题、相交弦问题以及它们的综合应用.解决这些问题经常转化为它们所对应的方程构成的方程组是否有解或解的个数问题.对相交弦长问题及中点弦问题要正确运用“设而不求”.涉及焦点弦的问题还可以利用圆锥曲线的焦半径公式.
●点击双基
5.在解题中,抛物线上的点、焦点、准线三者通常与抛物线的定义相联系,所以要注意相互转化.
拓展题例
[例题] (2003年北京东城区模拟题)已知抛物线C1:y2=4ax(a>0),椭圆C以原点为中心,以抛物线C1的焦点为右焦点,且长轴与短轴之比为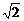 ,过抛物线C1的焦点F作倾斜角为
,过抛物线C1的焦点F作倾斜角为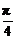 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
(1)求点P和Q的坐标;
(2)将点Q沿直线l向上移动到点Q′,使|QQ′|=4a,求过P和Q′且中心在原点,对称轴是坐标轴的双曲线的方程.
解:(1)由题意可知F(a,0),设椭圆方程为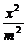 +
+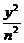 =1(m>n>0).
=1(m>n>0).

|
|

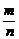 =
=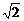 , m2=2a2,
, m2=2a2,
m2-n2=a2, n2=a2,
∴椭圆方程为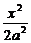 +
+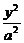 =1,直线l:y=x-a.
=1,直线l:y=x-a.
|
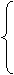 y=x-a,
y=x-a,
|
|
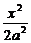 +
+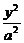 =1,
=1,
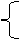
|
y2=4ax,
(2)将Q点沿直线l向上移动到Q′点,
使|QQ′|=4a,则可求出Q′点的坐标为(3a,2a).
设双曲线方程为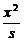 -
-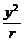 =1(s·r>0).
=1(s·r>0).
由于P、Q′在双曲线上,则有
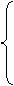
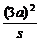 -
-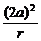 =1,
=1,
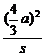 -
-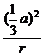 =1.
=1.
|
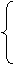
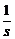 =
=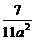 ,
,
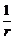 =
=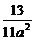 .
.
∴双曲线方程为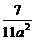 x2-
x2-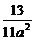 y2=1.
y2=1.
4.求抛物线方程时,要依据题设条件,弄清抛物线的对称轴和开口方向,正确地选择抛物线标准方程.
3.抛物线方程中,字母p的几何意义是抛物线的焦点F到准线的距离,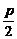 等于焦点到抛物线顶点的距离.牢记它对解题非常有益.
等于焦点到抛物线顶点的距离.牢记它对解题非常有益.
2.由于抛物线的离心率e=1,所以与椭圆及双曲线相比,它有许多特殊的性质,而且许多性质是可以借助于平面几何的知识来解决的.
1.圆锥曲线统一定义:平面内与一定点F和定直线l的距离之比为常数e的点的轨迹,当0<e<1时,表示椭圆;当e=1时,表示抛物线;当e>1时,表示双曲线.
3.解决焦点弦问题时,抛物线的定义有广泛的应用,而且还应注意焦点弦的几何性质.
●教师下载中心
教学点睛
本节重点是抛物线的定义、四种方程及几何性质.难点是四种方程的运用及对应性质的比较、辨别和应用,关键是定义的运用.建议在教学中注意以下几点:
2.凡涉及抛物线的弦长、弦的中点、弦的斜率问题时要注意利用韦达定理,能避免求交点坐标的复杂运算.
1.求抛物线方程时,若由已知条件可知曲线是抛物线,一般用待定系数法;若由已知条件可知曲线的动点的规律,一般用轨迹法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com