
4.注意“1”的灵活代换,如1=sin2α+cos2α=sec2α-tan2α=csc2α-cot2α=tanα·cotα.
3.注意公式的变形使用,弦切互化、三角代换、消元是三角变换的重要方法,要尽量减少开方运算,慎重确定符号.
2.在已知一个角的三角函数值,求这个角的其他三角函数值时,要注意题设中角的范围,并就不同的象限分别求出相应的值.
1.要熟悉任意角的概念、弧度制与角度制的互化、弧度制下的有关公式、任意角的三角函数概念.
10.是否存在α、β,α∈(-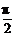 ,
,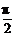 ),β∈(0,π)使等式sin(3π-α)=
),β∈(0,π)使等式sin(3π-α)=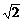 cos(
cos(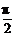 -β),
-β),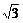 cos(-α)=-
cos(-α)=-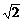 cos(π+β)同时成立?若存在,求出α、β的值;若不存在,请说明理由.
cos(π+β)同时成立?若存在,求出α、β的值;若不存在,请说明理由.
解:由条件得
①2+②2得sin2α+3cos2α=2,∴cos2α=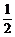 .
.
∵α∈(-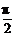 ,
,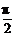 ),
),
∴α=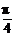 或α=-
或α=-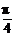 .
.
将α=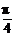 代入②得cosβ=
代入②得cosβ=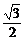 .又β∈(0,π),
.又β∈(0,π),
∴β=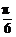 ,代入①可知,符合.
,代入①可知,符合.
将α=-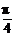 代入②得β=
代入②得β=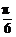 ,代入①可知,不符合.
,代入①可知,不符合.
综上可知α=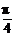 ,β=
,β=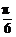 .
.
●思悟小结
9.设α∈(0,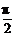 ),试证明:sinα<α<tanα.
),试证明:sinα<α<tanα.
证明:如下图,在平面直角坐标系中作单位圆,设角α以x轴正半轴为始边,终边与单位圆交于P点.
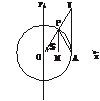
∵S△OPA<S扇形OPA<S△OAT,
∴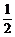 |MP|<
|MP|<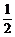 α<
α<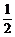 |AT|.
|AT|.
∴sinα<α<tanα.
探究创新
8.已知sinθ=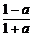 ,cosθ=
,cosθ=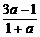 ,若θ是第二象限角,求实数a的值.
,若θ是第二象限角,求实数a的值.
解:依题意得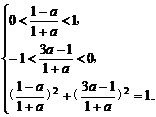
解得a=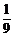 或a=1(舍去).
或a=1(舍去).
故实数a=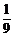 .
.
7.(2005年北京东城区模拟题)已知tan(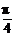 +α)=2,求:
+α)=2,求:
(1)tanα的值;
(2)sin2α+sin2α+cos2α的值.
(1)解:tan(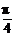 +α)=
+α)=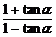 =2,∴tanα=
=2,∴tanα=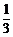 .
.
(2)解法一:sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α
=2sinαcosα+cos2α
=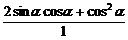 =
=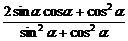
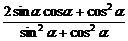 =
=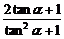 =
=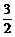 .
.
解法二:sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α
=2sinαcosα+cos2α. ①
∵tanα=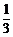 ,
,
∴α为第一象限或第三象限角.
当α为第一象限角时,sinα= ,cosα=
,cosα=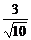 ,代入①得
,代入①得
2sinαcosα+cos2α=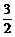 ;
;
当α为第三象限角时,sinα=- ,cosα=-
,cosα=-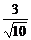 ,代入①得
,代入①得
2sinαcosα+cos2α=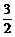 .
.
综上所述sin2α+sin2α+cos2α=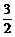 .
.
6.化简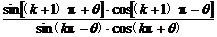 (k∈Z).
(k∈Z).
解:当k=2n(n∈Z)时,
原式=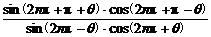
=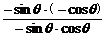 =-1.
=-1.
当k=2n+1(n∈Z)时,
原式=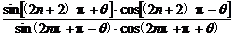
=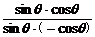 =-1.
=-1.
综上结论,原式=-1.
培养能力
5.若sinα·cosα<0,sinα·tanα<0,
化简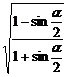 +
+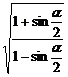 .
.
解:由所给条件知α是第二象限角,则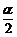 是第一或第三象限角.
是第一或第三象限角.
原式=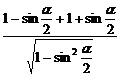 =
=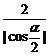
=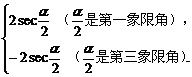
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com