
4.求定义域时,若需先把式子化简,一定要注意变形时x的取值范围不能发生变化.
●教师下载中心
教学点睛
解析式的求解中应引导学生用好图象,紧扣五点中的第一个零点,要注意图象的升降情况,注意数形结合的思想.
拓展题例
[例题] 已知函数f(x)=Asinωx+Bcosωx(A、B、ω是实常数,ω>0)的最小正周期为2,并当x=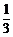 时,f(x)max=2.
时,f(x)max=2.
(1)求f(x).
(2)在闭区间[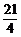 ,
,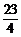 ]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,请说明理由.
解:(1)f(x)=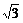 sinπx+cosπx=2sin(πx+
sinπx+cosπx=2sin(πx+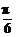 ).
).
(2)令πx+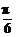 =kπ+
=kπ+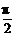 ,k∈Z.
,k∈Z.
∴x=k+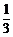 ,
,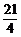 ≤k+
≤k+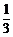 ≤
≤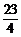 .
.
∴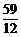 ≤k≤
≤k≤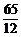 .∴k=5.
.∴k=5.
故在[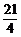 ,
,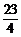 ]上只有f(x)的一条对称轴x=
]上只有f(x)的一条对称轴x=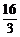 .
.
3.对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象.
2.作函数的图象时,首先要确定函数的定义域.
1.数形结合是数学中重要的思想方法,在中学阶段,对各类函数的研究都离不开图象,很多函数的性质都是通过观察图象而得到的.
9.(2004年北京西城区一模题)f(x)是定义在[-2π,2π]上的偶函数,当x∈[0,π]时,y=f(x)=cosx,当x∈(π,2π]时,f(x)的图象是斜率为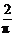 ,在y轴上截距为-2的直线在相应区间上的部分.
,在y轴上截距为-2的直线在相应区间上的部分.
(1)求f(-2π),f(- );
);
(2)求f(x),并作出图象,写出其单调区间.
解:(1)当x∈(π,2π]时,y=f(x)=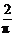 x-2,
x-2,
又f(x)是偶函数,∴f(-2π)=f(2π)=2.
又x∈[0,π]时,y=f(x)=cosx,
∴f(- )=f(
)=f( )=
)=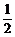 .
.
(2)y=f(x)=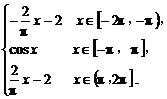
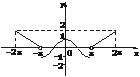
单调区间为[-2π,-π),[0,π),[-π,0],[π,2π].
●思悟小结
8.(2004年福建,17)设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,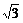 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1-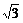 且x∈[-
且x∈[- ,
, ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<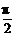 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
分析:本题主要考查平面向量的概念和计算、三角函数的恒等变换及其图象变换的基本技能,考查运算能力.
解:(1)依题设,f(x)=2cos2x+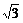 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+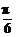 ).由1+2sin(2x+
).由1+2sin(2x+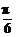 )=1-
)=1-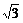 ,
,
得sin(2x+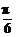 )=-
)=-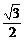 .
.
∵- ≤x≤
≤x≤ ,∴-
,∴-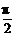 ≤2x+
≤2x+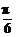 ≤
≤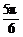 .
.
∴2x+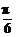 =-
=- ,即x=-
,即x=-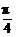 .
.
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(1)得f(x)=2sin2(x+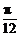 )+1.
)+1.
∵|m|<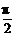 ,∴m=-
,∴m=-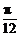 ,n=1.
,n=1.
探究创新
7.作出函数y=|sinx|+|cosx|,x∈[0,π]的图象,并写出函数的值域.
解:原式=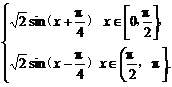
如下图:
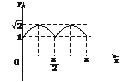
函数的值域为[1,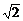 ].
].
6.画出函数y=|sinx|,y=sin|x|的图象.
解:y=sin|x|=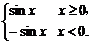
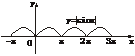
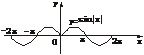
培养能力
5.(2004年上海,14)已知y=f(x)是周期为2π的函数,当x∈[0,2π)时,f(x)=sin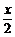 ,则f(x)=
,则f(x)=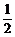 的解集为
的解集为
A.{x|x=2kπ+ ,k∈Z} B.{x|x=2kπ+
,k∈Z} B.{x|x=2kπ+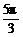 ,k∈Z}
,k∈Z}
C.{x|x=2kπ± ,k∈Z} D.{x|x=2kπ+(-1)k
,k∈Z} D.{x|x=2kπ+(-1)k  ,k∈Z}
,k∈Z}
解析:∵f(x)=sin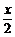 =
=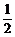 ,x∈[0,2π),
,x∈[0,2π),
∴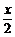 ∈[0,π).∴
∈[0,π).∴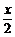 =
=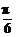 或
或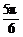 .
.
∴x= 或
或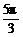 .
.
∵f(x)是周期为2π的周期函数,
∴f(x)=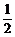 的解集为{x|x=2kπ±
的解集为{x|x=2kπ± ,k∈Z}.
,k∈Z}.
答案:C
4.函数y=Asin(x+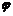 )与y=Acos(x+
)与y=Acos(x+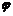 )在(x0,x0+π)上交点的个数为_______.
)在(x0,x0+π)上交点的个数为_______.
解析:画图象.
答案:1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com