
6.中心在坐标原点、焦点在x轴上的椭圆,它的离心率为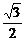 ,与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆方程.
,与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆方程.
解:设椭圆方程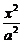 +
+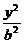 =1(a>b>0),
=1(a>b>0),
∵e=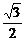 ,∴a2=4b2,即a=2b.
,∴a2=4b2,即a=2b.
∴椭圆方程为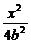 +
+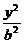 =1.
=1.
把直线方程代入化简得5x2-8x+4-4b2=0.
设M(x1,y1)、N(x2,y2),则
x1+x2=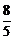 ,x1x2=
,x1x2=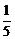 (4-4b2).
(4-4b2).
∴y1y2=(1-x1)(1-x2)
=1-(x1+x2)+x1x2=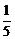 (1-4b2).
(1-4b2).
由于OM⊥ON,∴x1x2+y1y2=0.
解得b2=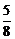 ,a2=
,a2=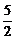 .
.
∴椭圆方程为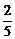 x2+
x2+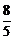 y2=1.
y2=1.
培养能力
5.求过点(0,2)的直线被椭圆x2+2y2=2所截弦的中点的轨迹方程.
解:设直线方程为y=kx+2,
把它代入x2+2y2=2,
整理得(2k2+1)x2+8kx+6=0.
要使直线和椭圆有两个不同交点,则Δ>0,即k<-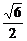 或k>
或k>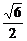 .
.
设直线与椭圆两个交点为A(x1,y1)、B(x2,y2),中点坐标为C(x,y),则
x=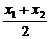 =
=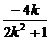 ,
,
y= 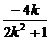 +2=
+2=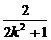 .
.
|
|
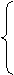 x=
x=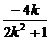 ,
,
y=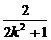
消去k得x2+2(y-1)2=2,
且|x|<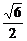 =,0<y<
=,0<y<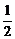 .
.
4.AB为抛物线y2=2px(p>0)的焦点弦,若|AB|=1,则AB中点的横坐标为___________;若AB的倾斜角为α,则|AB|=____________.
解析:设过F(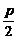 ,0)的直线为y=k(x-
,0)的直线为y=k(x-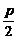 ),k≠0,代入抛物线方程,由条件可得结果.
),k≠0,代入抛物线方程,由条件可得结果.
答案: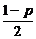
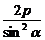
3.已知双曲线x2-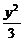 =1,过P(2,1)点作一直线交双曲线于A、B两点,并使P为AB的中点,则直线AB的斜率为____________.
=1,过P(2,1)点作一直线交双曲线于A、B两点,并使P为AB的中点,则直线AB的斜率为____________.
解析:设A(x1,y1)、B(x2,y2),代入双曲线方程3x2-y2=1相减得直线AB的斜率
kAB=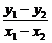 =
=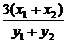
=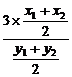 =
=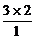 =6.
=6.
答案:6
2.已知对k∈R,直线y-kx-1=0与椭圆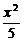 +
+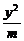 =1恒有公共点,则实数m的取值范围是
=1恒有公共点,则实数m的取值范围是
A.(0,1) B.(0,5)
C.[1,5)∪(5,+∞) D.[1,5)
解析:直线y-kx-1=0恒过点(0,1),仅当点(0,1)在椭圆上或椭圆内时,此直线才恒与椭圆有公共点.所以,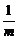 ≤1且m>0,得m≥1.故本题应选C.
≤1且m>0,得m≥1.故本题应选C.
答案:C
1.若双曲线x2-y2=1的右支上一点P(a,b)到直线y=x的距离为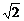 ,则a+b的值为
,则a+b的值为
A.-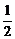 B.
B.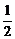 C.±
C.±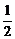 D.±2
D.±2
解析:P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.
d=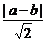 =
=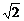 ,
,
∴|a-b|=2.
又P点在右支上,则有a>b,
∴a-b=2.
∴|a+b|×2=1,a+b=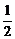 .
.
答案:B
5.已知(4,2)是直线l被椭圆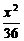 +
+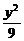 =1所截得的线段的中点,则l的方程是____________.
=1所截得的线段的中点,则l的方程是____________.
解析:设直线l与椭圆交于P1(x1,y1)、P2(x2,y2),
将P1、P2两点坐标代入椭圆方程相减得直线l斜率k=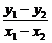 =-
=-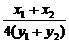 = -
= -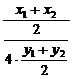
=-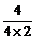 =-
=-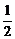 .
.
由点斜式可得l的方程为x+2y-8=0.
答案:x+2y-8=0
●典例剖析
[例1] 已知直线l:y=tanα(x+2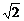 )交椭圆x2+9y2=9于A、B两点,若α为l的倾斜角,且|AB|的长不小于短轴的长,求α的取值范围.
)交椭圆x2+9y2=9于A、B两点,若α为l的倾斜角,且|AB|的长不小于短轴的长,求α的取值范围.
剖析:确定某一变量的取值范围,应设法建立关于这一变量的不等式,题设中已经明确给定弦长≥2b,最后可归结为计算弦长求解不等式的问题.
解:将l方程与椭圆方程联立,消去y,得(1+9tan2α)x2+36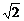 tan2α·x+72tan2α-9=0,
tan2α·x+72tan2α-9=0,
∴|AB|=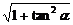 |x2-x1|
|x2-x1|
=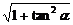 ·
·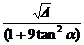
=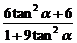 .
.
由|AB|≥2,得tan2α≤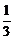 ,
,
∴-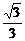 ≤tanα≤
≤tanα≤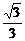 .
.
∴α的取值范围是[0,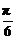 )∪[
)∪[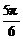 ,π).
,π).
评述:对于弦长公式一定要能熟练掌握、灵活运用.本题由于l的方程由tanα给出,所以可以认定α≠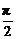 ,否则涉及弦长计算时,还应讨论α=
,否则涉及弦长计算时,还应讨论α=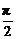 时的情况.
时的情况.
深化拓展
本题若把条件|AB|的长不小于短轴的长去掉,改为求|AB|的长的取值范围.读者不妨一试.
提示:|AB|=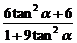 ,
,
设|AB|=y,即y=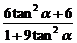 ,
,
9ytan2α+y=6tan2α+6,
(9y-6)tan2α+y-6=0.
当y≠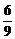 时,由Δ≥0得
时,由Δ≥0得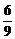 <y≤6.
<y≤6.
当y=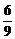 时,l与x轴垂直,
时,l与x轴垂直,
故|AB|的范围是[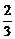 ,6].
,6].
[例2] 已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点.
(1)求证:OA⊥OB;
(2)当△OAB的面积等于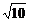 时,求k的值.
时,求k的值.
剖析:证明OA⊥OB可有两种思路(如下图):
(1)证kOA·kOB=-1;
(2)取AB中点M,证|OM|=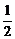 |AB|.
|AB|.
求k的值,关键是利用面积建立关于k的方程,求△AOB的面积也有两种思路:
(1)利用S△OAB=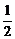 |AB|·h(h为O到AB的距离);
|AB|·h(h为O到AB的距离);
(2)设A(x1,y1)、B(x2,y2),直线和x轴交点为N,利用S△OAB=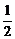 |AB|·|y1-y2|.
|AB|·|y1-y2|.
请同学们各选一种思路给出解法.
解方程组时,是消去x还是消去y,这要根据解题的思路去确定.当然,这里消去x是最简捷的.
(1)证明:如下图,由方程组
|
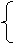 y2=-x,
y2=-x,
y=k(x+1)
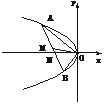
ky2+y-k=0.
设A(x1,y1)、B(x2,y2),由韦达定理y1·y2=-1.
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12·y22=x1x2.
∵kOA·kOB=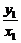 ·
·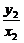 =
=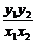 =
=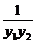 =-1,
=-1,
∴OA⊥OB.
(2)解:设直线与x轴交于N,又显然k≠0,
∴令y=0,则x=-1,即N(-1,0).
∵S△OAB=S△OAN+S△OBN
=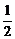 |ON||y1|+
|ON||y1|+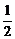 |ON||y2|
|ON||y2|
=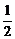 |ON|·|y1-y2|,
|ON|·|y1-y2|,
∴S△OAB=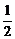 ·1·
·1·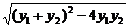
=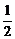
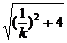 .
.
∵S△OAB=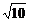 ,
,
∴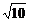 =
=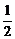
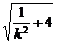 .解得k=±
.解得k=±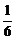 .
.
评述:本题考查了两直线垂直的充要条件、三角形的面积公式、函数与方程的思想,以及分析问题、解决问题的能力.
[例3] 在抛物线y2=4x上恒有两点关于直线y=kx+3对称,求k的取值范围.
剖析:设B、C两点关于直线y=kx+3对称,易得直线BC:x=-ky+m,由B、C两点关于直线y=kx+3对称可得m与k的关系式,
而直线BC与抛物线有两交点,
∴Δ>0,即可求得k的范围.
解:设B、C关于直线y=kx+3对称,直线BC方程为x=-ky+m,代入y2=4x,得y2+4ky-4m=0,
设B(x1,y1)、C(x2,y2),BC中点M(x0,y0),
则y0=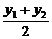 =-2k,x0=2k2+m.
=-2k,x0=2k2+m.
∵点M(x0,y0)在直线l上,
∴-2k=k(2k2+m)+3.
∴m=-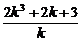 .
.
又∵BC与抛物线交于不同两点,
∴Δ=16k2+16m>0.
把m代入化简得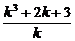 <0,
<0,
即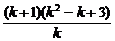 <0,解得-1<k<0.
<0,解得-1<k<0.
评述:对称问题是高考的热点之一,由对称易得两个关系式.本题运用了“设而不求”,解决本题的关键是由B、C两点在抛物线上得“Δ>0”.
思考讨论
将直线BC设为x=-ky+m.好!若直线BC的方程设为y=-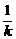 x+m,本题运算量增大,同学们不妨一试.
x+m,本题运算量增大,同学们不妨一试.
●闯关训练
夯实基础
4.过抛物线y2=4x焦点的直线交抛物线于A、B两点,已知|AB|=8,O为坐标原点,则 △OAB的重心的横坐标为____________.
解析:由题意知抛物线焦点F(1,0).设过焦点F(1,0)的直线为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2).
代入抛物线方程消去y得k2x2-2(k2+2)x+k2=0.
∵k2≠0,∴x1+x2=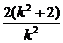 ,x1x2=1.
,x1x2=1.
∵|AB|=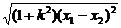
=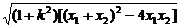
=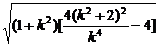
=8,
∴k2=1.
∴△OAB的重心的横坐标为x=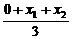 =2.
=2.
答案:2
3.双曲线x2-y2=1的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是
A.(-∞,0)
B.(1,+∞)
C.(-∞,0)∪(1,+∞)
D.(-∞,-1)∪(1,+∞)
解析:数形结合法,与渐近线斜率比较.
答案:C
2.已知双曲线C:x2-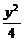 =1,过点P(1,1)作直线l,使l与C有且只有一个公共点,则满足上述条件的直线l共有
=1,过点P(1,1)作直线l,使l与C有且只有一个公共点,则满足上述条件的直线l共有
A.1条 B.2条 C.3条 D.4条
解析:数形结合法,与渐近线平行、相切.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com