
1.直线与直线、直线与平面、平面与平面的位置关系.
3.注意用好以下数学思想、方法:
①方程思想;②函数思想;③对称思想;④参数思想;⑤转化思想;⑥分类思想.
除上述几种常用数学思想外,整体思想、数形结合思想、主元分析思想、正难则反思想、构造思想等也是解析几何解题中不可缺少的思想方法.在复习中必须给予足够的重视,真正发挥数学解题思想作为联系知识与能力中的作用,从而提高简化计算能力.
●教师下载中心
教学点睛
本节是圆锥曲线的综合应用,主要是曲线方程的运用、变量范围的计算、最值的确定等,解决这类问题的关键是依据解析几何本身的特点,寻找一个突破口,那么如何找到解决问题的突破口呢?
(1)结合定义利用图形中几何量之间的大小关系.(2)建立目标函数,转化为求函数的最值问题.(3)利用代数基本不等式.代数基本不等式的应用,往往需要创造条件,并进行巧妙的构思.(4)结合参数方程,利用三角函数的有界性.直线、圆或椭圆的参数方程,它们的一个共同特点是均含有三角式.因此,它们的应用价值在于:①通过参数θ简明地表示曲线上点的坐标;②利用三角函数的有界性及其变形公式来帮助求解诸如最值、范围等问题. (5)构造一个二次方程,利用判别式Δ≥0.
拓展题例
[例1] (2005年启东市第二次调研题)抛物线y2=4px(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),求证:x0>3p;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,当0<p<1时,求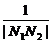 +
+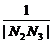 +…+
+…+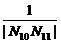 的值.
的值.
(1)证明:设直线l方程为y=k(x+p),代入y2=4px.
得k2x2+(2k2p-4p)x+k2p2=0.
Δ=4(k2p-2p)2-4k2·k2p2>0,
得0<k2<1.
令A(x1,y1)、B(x2,y2),则x1+x2=-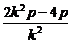 ,y1+y2=k(x1+x2+2p)=
,y1+y2=k(x1+x2+2p)=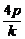 ,
,
AB中点坐标为(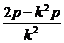 ,
,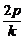 ).
).
AB垂直平分线为y-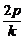 =-
=-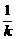 (x-
(x-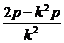 ).
).
令y=0,得x0=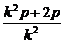 =p+
=p+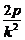 .
.
由上可知0<k2<1,∴x0>p+2p=3p.
∴x0>3p.
(2)解:∵l的斜率依次为p,p2,p3,…时,AB中垂线与x轴交点依次为N1,N2,N3,…(0<p<1).
∴点Nn的坐标为(p+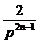 ,0).
,0).
|NnNn+1|=|(p+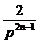 )-(p+
)-(p+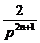 )|=
)|=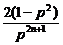 ,
,
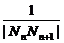 =
=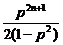 ,
,
所求的值为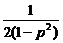 [p3+p4+…+p21]=
[p3+p4+…+p21]=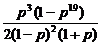 .
.
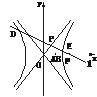
[例2] (2003年南京市模拟题)已知双曲线C: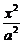 -
-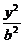 =1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足|
=1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足|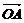 |、|
|、|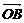 |、|
|、|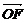 |成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.
|成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.
(1)求证: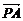 ·
·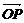 =
=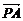 ·
·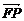 ;
;
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.
(1)证法一:
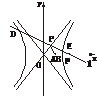
l:y=-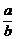 (x-c).
(x-c).
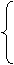 y=-
y=-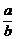 (x-c),
(x-c),
y=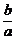 x.
x.
解得P(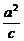 ,
,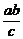 ).∵|
).∵|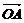 |、|
|、|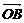 |、|
|、|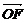 |成等比数列,∴A(
|成等比数列,∴A(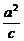 ,0).
,0).
∴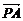 =(0,-
=(0,-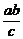 ),
),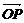 =(
=(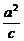 ,
,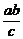 ),
),
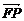 =(-
=(-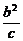 ,
,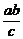 ).
).
∴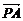 ·
·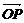 =-
=-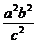 ,
,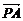 ·
·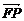 =-
=-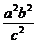 .
.
∴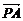 ·
·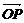 =
=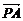 ·
·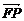 .
.
证法二:同上得P(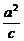 ,
,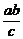 ).
).
∴PA⊥x轴,
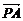 ·
·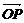 -
-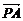 ·
·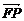 =
=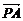 ·
·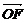 =0.
=0.
∴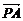 ·
·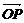 =
=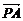 ·
·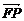 .
.
|
 y=-
y=-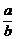 (x-c),
(x-c),
b2x2-a2y2=a2b2.
∴b2x2-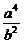 (x-c)2=a2b2,
(x-c)2=a2b2,
即(b2-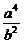 )x2+2
)x2+2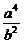 cx-(
cx-(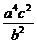 +a2b2)=0.
+a2b2)=0.
∵x1·x2=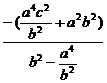 <0,
<0,
∴b4>a4,
即b2>a2,c2-a2>a2.
∴e2>2,即e>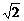 .
.
2.四点重视:①重视定义在解题中的作用;②重视平面几何知识在解题中的简化功能;③重视根与系数关系在解题中的作用;④重视曲线的几何特征与方程的代数特征的统一.
1.客观题求解时应注意画图,抓住涉及到的一些元素的几何意义,用数形结合法去分析解决.
9.(2005年春季上海,22)(1)求右焦点坐标是(2,0),且经过点(-2,-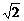 )的椭圆的标准方程.
)的椭圆的标准方程.
(2)已知椭圆C的方程是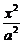 +
+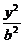 =1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.
=1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.

(1)解:设椭圆的标准方程为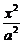 +
+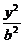 =1,a>b>0,
=1,a>b>0,
∴a2=b2+4,即椭圆的方程为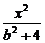 +
+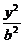 =1.
=1.
∵点(-2,-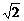 )在椭圆上,
)在椭圆上,
∴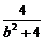 +
+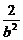 =1.
=1.
解得b2=4或b2=-2(舍).
由此得a2=8,即椭圆的标准方程为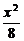 +
+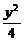 =1.
=1.
(2)证明:设直线l的方程为y=kx+m,
与椭圆C的交点A(x1,y1)、B(x2,y2),
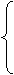 y=kx+m,
y=kx+m,
|
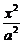 +
+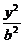 =1.
=1.
解得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
∵Δ>0,∴m2<b2+a2k2,
即-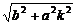 <m<
<m<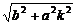 .
.
则x1+x2=-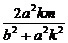 ,y1+y2=kx1+m+kx2+m=
,y1+y2=kx1+m+kx2+m=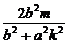 ,
,
∴AB中点M的坐标为(-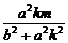 ,
,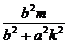 ).
).
∴线段AB的中点M在过原点的直线b2x+a2ky=0上.
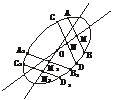
(3)解:如下图,作两条平行直线分别交椭圆于A、B和C、D,并分别取AB、CD的中点M、N,连结直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于A1、B1和C1、D1,并分别取A1B1、C1D1的中点M1、N1,连结直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心.
●思悟小结
在知识的交汇点处命题,是高考命题的趋势,而解析几何与函数、三角、数列、向量等知识的密切联系,正是高考命题的热点,为此在学习时应抓住以下几点:
8.(2003年北京东城区模拟题)从椭圆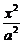 +
+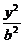 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上端点B的连线AB∥OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上端点B的连线AB∥OM.
(1)求椭圆的离心率;
(2)若Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围;
(3)过F1作AB的平行线交椭圆于C、D两点,若|CD|=3,求椭圆的方程.
解:(1)由已知可设M(-c,y),
则有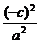 +
+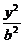 =1.
=1.
∵M在第二象限,∴M(-c,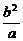 ).
).
又由AB∥OM,可知kAB=kOM.
∴-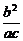 =-
=-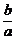 .∴b=c.∴a=
.∴b=c.∴a=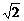 b.
b.
∴e=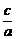 =
=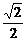 .
.
(2)设|F1Q|=m,|F2Q|=n,
则m+n=2a,mn>0.|F1F2|=2c,a2=2c2,
∴cos∠F1QF2=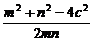
=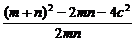 =
=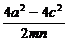 -1
-1
=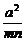 -1≥
-1≥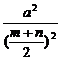 -1=
-1=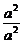 -1=0.
-1=0.
当且仅当m=n=a时,等号成立.
故∠F1QF2∈[0,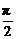 ].
].
(3)∵CD∥AB,kCD=-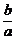 =-
=-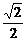 .
.
设直线CD的方程为y=-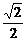 (x+c),
(x+c),
即y=-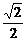 (x+b).
(x+b).
|
|
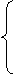
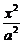 +
+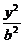 =1,
=1,
y=-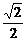 (x+b).
(x+b).
(a2+2b2)x2+2a2bx-a2b2=0.
设C(x1,y1)、D(x2,y2),∵a2=2b2,
∴x1+x2=-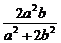 =-
=-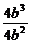 =-b,
=-b,
x1·x2=-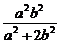 =-
=-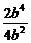 =-
=-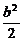 .
.
∴|CD|=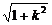 |x1-x2|
|x1-x2|
=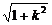 ·
·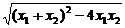
=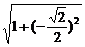 ·
·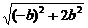 =
=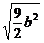 =3.
=3.
∴b2=2,则a2=4.
∴椭圆的方程为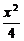 +
+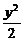 =1.
=1.
探究创新
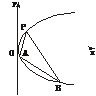
7.(理)(2004年北京,17)如下图,过抛物线y2=2px(p>0)上一定点P(x0,y0) (y0>0),作两条直线分别交抛物线于A(x1,y1)、B(x2,y2).
(1)求该抛物线上纵坐标为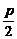 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求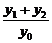 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
解:(1)当y=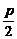 时,x=
时,x=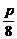 .
.
又抛物线y2=2px的准线方程为x=-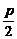 ,
,
由抛物线定义得
所求距离为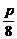 -(-
-(-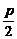 )=
)=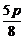 .
.
(2)设直线PA的斜率为kPA,直线PB的斜率为kPB.
由y12=2px1,y02=2px0,
相减得(y1-y0)(y1+y0)=2p(x1-x0),
故kPA= =
=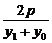 (x1≠x0).
(x1≠x0).
同理可得kPB=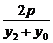 (x2≠x0).
(x2≠x0).
由PA、PB倾斜角互补知kPA=-kPB,
即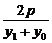 =-
=-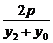 ,所以y1+y2=-2y0,
,所以y1+y2=-2y0,
故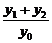 =-2.
=-2.
设直线AB的斜率为kAB.
由y22=2px2,y12=2px1,
相减得(y2-y1)(y2+y1)=2p(x2-x1),
所以kAB=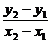 =
=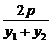 (x1≠x2).
(x1≠x2).
将y1+y2=-2y0(y0>0)代入得
kAB=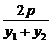 =-
=-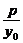 ,所以kAB是非零常数.
,所以kAB是非零常数.
(文)如下图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.

(1)写出该抛物线的方程及其准线方程;
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
解:(1)由已知条件,可设抛物线的方程为y2=2px.∵点P(1,2)在抛物线上,
∴22=2p·1,得p=2.
故所求抛物线的方程是y2=4x,准线方程是x=-1.
(2)设直线PA的斜率为kPA,直线PB的斜率为kPB.
则kPA=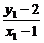 (x1≠1),kPB=
(x1≠1),kPB=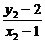 (x2≠1).
(x2≠1).
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB.
由A(x1,y1)、B(x2,y2)在抛物线上,得
y12=4x1, ①
y22=4x2, ②
∴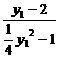 =-
=-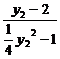 .
.
∴y1+2=-(y2+2).∴y1+y2=-4.
由①-②得直线AB的斜率
kAB=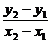 =
=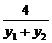 =-
=-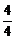 =-1(x1≠x2).
=-1(x1≠x2).
6.(2003年湖北八市模拟题)已知抛物线y2=2px上有一内接正△AOB,O为坐标原点.
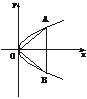
(1)求证:点A、B关于x轴对称;
(2)求△AOB外接圆的方程.
(1)证明:设A(x1,y1)、B(x2,y2),
∵|OA|=|OB|,∴x12+y12=x22+y22.
又∵y12=2px1,y22=2px2,
∴x22-x12+2p(x2-x1)=0,
即(x2-x1)(x1+x2+2p)=0.
又∵x1、x2与p同号,∴x1+x2+2p≠0.
∴x2-x1=0,即x1=x2.
由抛物线对称性,知点A、B关于x轴对称.
(2)解:由(1)知∠AOx=30°,则
|
 y2=2px, x=6p,
y2=2px, x=6p,
y=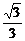 x y=2
x y=2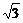 p.
p.
∴A(6p,2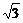 p).
p).
方法一:待定系数法,△AOB外接圆过原点O,且圆心在x轴上,可设其方程为x2+y2+dx=0.
将点A(6p,2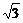 p)代入,得d=-8p.
p)代入,得d=-8p.
故△AOB外接圆方程为x2+y2-8px=0.
方法二:直接求圆心、半径,设半径为r,则圆心(r,0).
培养能力
5.(1)试讨论方程(1-k)x2+(3-k2)y2=4(k∈R)所表示的曲线;
(2)试给出方程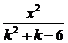 +
+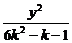 =1表示双曲线的充要条件.
=1表示双曲线的充要条件.
解:(1)3-k2>1-k>0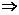 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0
k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0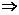 k∈(-
k∈(-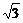 ,-1),方程所表示的曲线是焦点在y轴上的椭圆;1-k=3-k2>0
,-1),方程所表示的曲线是焦点在y轴上的椭圆;1-k=3-k2>0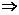 k=-1,表示的是一个圆;(1-k)(3-k2)<0
k=-1,表示的是一个圆;(1-k)(3-k2)<0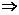 k∈(-∞,-
k∈(-∞,-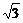 )∪(1,
)∪(1,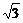 ),表示的是双曲线;k=1,k=-
),表示的是双曲线;k=1,k=-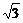 ,表示的是两条平行直线;k=
,表示的是两条平行直线;k=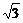 ,表示的图形不存在.
,表示的图形不存在.
(2)由(k2+k-6)(6k2-k-1)<0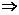 (k+3)(k-2)(3k+1)(2k-1)<0
(k+3)(k-2)(3k+1)(2k-1)<0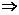 k∈(-3,-
k∈(-3,-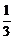 )∪(
)∪(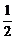 ,2).
,2).
4.(2004年全国Ⅱ,15)设中心在原点的椭圆与双曲线2x2-2y2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是_________________.
解析:双曲线中,a=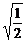 =b,∴F(±1,0),e=
=b,∴F(±1,0),e=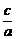 =
=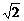 .∴椭圆的焦点为(±1,0),离心率为
.∴椭圆的焦点为(±1,0),离心率为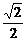 .∴长半轴长为
.∴长半轴长为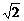 ,短半轴长为1.
,短半轴长为1.
∴方程为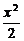 +y2=1.
+y2=1.
答案: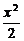 +y2=1
+y2=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com