
6.如下图,在△ABC中,∠ACB=90°,AB=8,∠BAC=60°,PC⊥平面ABC,PC=4,M为AB边上的一个动点,求PM的最小值.
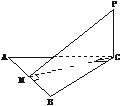
解:∵P是定点,要使PM的值最小,只需使PM⊥AB即可.
要使PM⊥AB,由于PC⊥平面ABC,
∴只需使CM⊥AB即可.
∵∠BAC=60°,AB=8,
∴AC=AB·cos60°=4.
∴CM=AC·sin60°=4·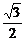 =2
=2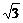 .
.
∴PM=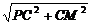 =
=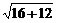 =2
=2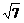 .
.
5.在三棱锥S-ABC中,N是S在底面ABC上的射影,且N在△ABC的AB边的高CD上,点M∈SC,截面MAB和底面ABC所成的二面角M-AB-C等于∠NSC,求证:SC⊥截面MAB.
证明:∵CD是SC在底面ABC上的射影,AB⊥CD,∴AB⊥SC.连结MD.∵∠MDC=
∠NSC,∴DM⊥SC.∵AB∩DM=D,∴SC⊥截面MAB.
培养能力
4.如下图,在正方体ABCD-A1B1C1D1中,M为CC1的中点,AC交BD于点O,求证:A1O⊥平面MBD.
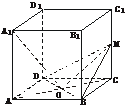
证明:连结MO.
∵DB⊥A1A,DB⊥AC,A1A∩AC=A,
∴DB⊥平面A1ACC1.
又A1O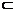 平面A1ACC1,∴A1O⊥DB.
平面A1ACC1,∴A1O⊥DB.
在矩形A1ACC1中,tan∠AA1O=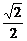 ,
,
tan∠MOC=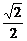 ,∴∠AA1O=∠MOC,
,∴∠AA1O=∠MOC,
则∠A1OA+∠MOC=90°.∴A1O⊥OM.
∵OM∩DB=O,∴A1O⊥平面MBD.
3.Rt△ABC在平面α内的射影是△A1B1C1,设直角边AB∥α,则△A1B1C1的形状是_____________三角形.
解析:根据两平行平面的性质及平行角定理,知△A1B1C的形状仍是Rt△.
答案:直角
2.△ABC的三个顶点A、B、C到平面α的距离分别为2 cm、3 cm、4 cm,且它们在α的同侧,则△ABC的重心到平面α的距离为_____________.
解析:如下图,设A、B、C在平面α上的射影分别为A′、B′、C′,△ABC的重心为G,连结CG交AB于中点E,又设E、G在平面α上的射影分别为E′、G′,则E′∈A′B,G′∈C′E,EE′=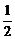 (A′A+B′B)=
(A′A+B′B)=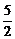 ,CC′=4,CG∶GE=2∶1,
,CC′=4,CG∶GE=2∶1,
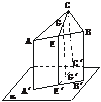
在直角梯形EE′C′C中可求得GG′=3.
答案:3 cm
1.PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任一点,则下列关系不正确的是
A.PA⊥BC B.BC⊥平面PAC C.AC⊥PB D.PC⊥BC
解析:由三垂线定理知AC⊥PB,故选C.
答案:C
5.设正方体ABCD-A1B1C1D1的棱长为1,则
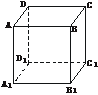
(1)A点到CD1的距离为________;
(2)A点到BD1的距离为________;
(3)A点到面BDD1B1的距离为_____________;
(4)A点到面A1BD的距离为_____________;
(5)AA1与面BB1D1D的距离为__________.
答案:(1)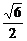 (2)
(2)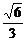 (3)
(3)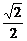 (4)
(4)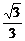 (5)
(5)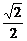
●典例剖析
[例1] 已知直线a⊥平面α,直线b⊥平面α,O、A为垂足.求证:a∥b.
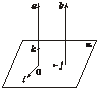
证明:以O为原点直线a为z轴,建立空间直角坐标系,i、j、k为坐标向量,直线a、b的向量分别为a、b.设b=(x,y,z),∵b⊥α,∴b·i=x=0,b·j=y=0,b=(0,0,z)=zk.∴b∥k,a∥b.
评述:因证明两直线平行,也就是证明其方向向量共线,所以,利用两向量共线的充要条件证明两直线平行是新教材基本的数学方法,应做到熟练运用.
[例2] 已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A点作AE⊥PC于点E,求证:AE⊥平面PBC.
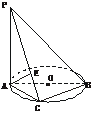
证明:∵PA⊥平面ABC,∴PA⊥BC.
又∵AB是⊙O的直径,∴BC⊥AC.而PC∩AC=C,∴BC⊥平面PAC.
又∵AE在平面PAC内,∴BC⊥AE.
∵PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
思考讨论
证明直线与平面垂直的常用方法有:利用线面垂直的定义;利用线面垂直的判定定理;利用“若直线a∥直线b,直线a⊥平面α,则直线b⊥平面α”.
[例3] 在直三棱柱ABC-A1B1C1中,B1C1=A1C1,A1B⊥AC1,求证:A1B⊥B1C.
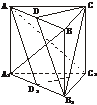
证明:取A1B1的中点D1,连结C1D1.
∵B1C1=A1C1,∴C1D1⊥ABB1A1.
连结AD1,则AD1是AC1在平面ABB1A1内的射影,
∵A1B⊥AC1,
∴A1B⊥AD1.取AB的中点D,连结CD、B1D,则B1D∥AD1,且B1D是B1C在平面ABB1A1内的射影.
∵B1D⊥A1B,∴A1B⊥B1C.
思考讨论
证明异面直线垂直的常用方法有:证明其中一直线垂直于另外一直线所在的平面;利用三垂线定理及其逆定理.
●闯关训练
夯实基础
4.在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件_____________时,有A1C⊥B1D1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
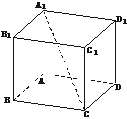
答案:A1C1⊥B1D1或四边形A1B1C1D1为菱形等
3.在正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,D是EF的中点,沿SE、SF及EF把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G,那么,在四面体S-EFG中必有
A.SG⊥平面EFG B.SD⊥平面EFG C.FG⊥平面SEF D.GD⊥平面SEF
解析:注意折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,即SG⊥GE,SG⊥GF,所以SG⊥
平面EFG.选A.
答案:A
2.给出下列命题,其中正确的两个命题是
①直线上有两点到平面的距离相等,则此直线与平面平行 ②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m⊥平面α,直线n⊥m,则n∥α ④a、b是异面直线,则存在唯一的平面α,使它与a、b都平行且与a、b距离相等
A.①② B.②③ C.③④ D.②④
解析:①错误.如果这两点在该平面的异侧,则直线与平面相交.②正确.如下图,平面α∥β,A∈α,C∈α,D∈β,B∈β且E、F分别为AB、CD的中点,过C作CG∥AB交平面β于G,连结BG、GD.
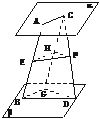
设H是CG的中点,则EH∥BG,HF∥GD.
∴EH∥平面β,HF∥平面β.
∴平面EHF∥平面β∥平面α.
∴EF∥α,EF∥β.
③错误.直线n可能在平面α内.
④正确.如下图,设AB是异面直线a、b的公垂线段,E为AB的中点,过E作a′∥a,b′∥b,则a′、b′确定的平面即为与a、b都平行且与a、b距离相等的平面,并且它是唯一确定的.
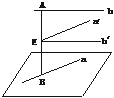
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com