
8.有点难度哟!
(2003年天津质量检测题)已知适合不等式|x2-4x+a|+|x-3|≤5的x的最大值为3,求实数a的值,并解该不等式.
解:∵x≤3,∴|x-3|=3-x.
若x2-4x+a<0,则原不等式化为x2-3x+a+2≥0.
此不等式的解集不可能是集合{x|x≤3}的子集,∴x2-4x+a<0不成立.
于是,x2-4x+a≥0,则原不等式化为x2-5x+a-2≤0.∵x≤3,
令x2-5x+a-2=(x-3)(x-m)=x2-(m+3)x+3m,比较系数,得m=2,∴a=8.
此时,原不等式的解集为{x|2≤x≤3}.
探究创新
7.(2004年春季安徽)解关于x的不等式loga3x<3logax(a>0,且a≠1).
解:令y=logax,则原不等式化为y3-3y<0,
解得y<-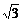 或0<y<
或0<y<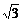 ,
,
即logax<-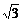 或0<logax<
或0<logax<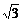 .
.
当0<a<1时,不等式的解集为{x|x>a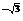 }∪{x|a
}∪{x|a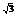 <x<1};
<x<1};
当a>1时,不等式的解集为{x|0<x<a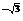 }∪{x|1<x<a
}∪{x|1<x<a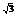 }.
}.
6.(2003年北京西城区一模题)解关于x的不等式ax2-2≥2x-ax(a∈R).
解:原不等式变形为ax2+(a-2)x-2≥0.
①a=0时,x≤-1;
②a≠0时,不等式即为(ax-2)(x+1)≥0,
当a>0时,x≥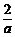 或x≤-1;
或x≤-1;
由于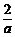 -(-1)=
-(-1)=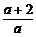 ,于是
,于是
当-2<a<0时,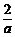 ≤x≤-1;
≤x≤-1;
当a=-2时,x=-1;
当a<-2时,-1≤x≤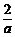 .
.
综上,当a=0时,x≤-1;当a>0时,x≥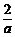 或x≤-1;当-2<a<0时,
或x≤-1;当-2<a<0时,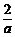 ≤x≤-1;
≤x≤-1;
当a=-2时,x=-1;当a<-2时,-1≤x≤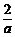 .
.
培养能力
5.(2004年宣武二模题)定义符号函数sgnx=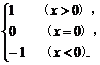 当x∈R时,解不等式(x+2)>(2x-1)sgnx.
当x∈R时,解不等式(x+2)>(2x-1)sgnx.
解:当x>0时,原不等式为x+2>2x-1.
∴0<x<3.
当x=0时,成立.
当x<0时,x+2>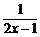 .
.
x-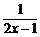 +2>0.
+2>0.
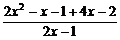 >0.
>0.
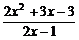 >0.∴-
>0.∴-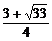 <x<0.
<x<0.
综上,原不等式的解集为{x|-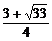 <x<3}.
<x<3}.
4.(2004年浙江,13)已知f(x)=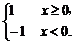 则不等式x+(x+2)·f(x+2)≤5的解集是____________.
则不等式x+(x+2)·f(x+2)≤5的解集是____________.
解析:当x+2≥0,即x≥-2时.
x+(x+2)f(x+2)≤5
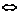 2x+2≤5
2x+2≤5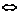 x≤
x≤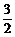 .
.
∴-2≤x≤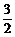 .
.
当x+2<0即x<-2时,x+(x+2)f(x+2)≤5
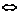 x+(x+2)·(-1)≤5
x+(x+2)·(-1)≤5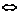 -2≤5,
-2≤5,
∴x<-2.
综上x≤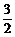 .
.
答案:(-∞,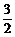 ]
]
3.若关于x的不等式-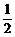 x2+2x>mx的解集为{x|0<x<2},则实数m的值为_______.
x2+2x>mx的解集为{x|0<x<2},则实数m的值为_______.
解析:由题意,知0、2是方程-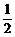 x2+(2-m)x=0的两个根,
x2+(2-m)x=0的两个根,
∴-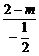 =0+2.∴m=1.
=0+2.∴m=1.
答案:1
2.设f(x)和g(x)都是定义域为R的奇函数,不等式f(x)>0的解集为(m,n),不等式g(x)>0的解集为(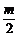 ,
,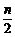 ),其中0<m<
),其中0<m<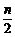 ,则不等式f(x)·g(x)>0的解集是
,则不等式f(x)·g(x)>0的解集是
A.(m,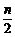 ) B.(m,
) B.(m,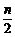 )∪(-
)∪(-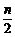 ,-m)
,-m)
C.(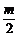 ,
,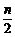 )∪(-n,-m) D.(
)∪(-n,-m) D.(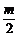 ,
,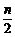 )∪(-
)∪(-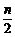 ,-
,-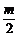 )
)
解析:f(x)、g(x)都是定义域为R的奇函数,f(x)>0的解集为(m,n),g(x)>0的解集为(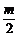 ,
,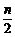 ).
).
∴f(-x)>0的解集为(-n,-m),g(-x)>0的解集为(-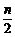 ,-
,-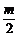 ),
),
即f(x)<0的解集为(-n,-m),g(x)<0的解集为(-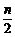 ,-
,-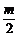 ).
).
由f(x)·g(x)>0得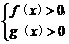 或
或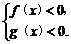 .又0<m<
.又0<m<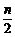 ,
,
∴m<x<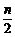 或-
或-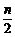 <x<-m.
<x<-m.
答案:B
1.(2004年重庆,4)不等式x+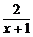 >2的解集是
>2的解集是
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
C.(-1,0)∪(0,1) D.(-∞,-1)∪(1,+∞)
解法一:x+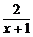 >2
>2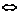 x-2+
x-2+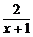 >0
>0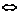
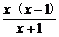 >0
>0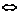 x(x-1)(x+1)>0
x(x-1)(x+1)>0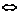 -1<x<0或x>1.
-1<x<0或x>1.
解法二:验证,x=-2、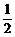 不满足不等式,排除B、C、D.
不满足不等式,排除B、C、D.
答案:A
2.本题若把m分离出来再求m的范围能行吗?
●闯关训练
夯实基础
1.本题若变式:不等式2x-1>m(x2-1)对一切-2≤x≤2都成立,求m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com