Pythagores     Descartes

随社会的发展，分配及更精确丈量土地的需要，正整数已不够用，人们引进了分数。世界上最早有关分数的记载，要数埃及的纸草文书，但迟至公元前1650年的Ahmes所著的《获得一切奥秘的指南》，仍将分数化成分子是1再加以计算；我国在公元前100年的《周髀算经》中就有了具体分数的计算，在其后的《孙子算经》及《九章算术》中就明确总结了分数的计算、表示方法，（只不过当时分数的表示方法是分子在上、分母在下、中间无横线，且带分数的整数部分又排在最上面）。现今的分数表示法，迟至1175年中亚西亚的Al-Hassan才在其著作中出现，同时十进制分数西传过程中与印度文化相结合，如：叙利亚的Al-Battanl于十世纪引入正切、余切时采用了小数，使分数在编译过程中改进为另一面貌形式。

负数及运算法则也是我国最先引入的：在《九章算术》中，以收入、余钱、入帐为正，付款、不足、减掉为负，并系统阐述了加减的运算法则，因该书是对前人经验的总结，因此实质负数及其运算规则比它要早些；至1299年，朱世杰编的《算学启蒙》中有了负数乘除法的法则。欧洲对负数的处理是由意大利的Fibonacci提出后又不敢承认，一段时间内将之视作“假数”或“荒诞的数”，至Bcmbell才给出明确的定义，Girdrd将负数与正数等量齐观，并用“-”表示负数，一直沿用至今。

三，跌宕起伏的无理数

远在公元前500年左右，古希腊著名的Pythagores学派就认为：“万物皆数，数皆可归为整数或整数之比，此比称公度比”，即现在的正有理数（因当时欧洲还没有负数及零的概念）；但在公元前五世纪时，该学派的一名成员Hippasus发现：“正方形的对角线与其一边无公度比”，这一发现使该学派成员大为惊慌――居然有人敢反对伟大的Pythagores！在争论和大家的愤怒声讨中，犯了众怒的Hippasus被抛入大海。

人类最初只有“无”与“有”这两个描写一天有无猎物或是否见到同伴的词。后来，从“有”中分化出“多”与“少”等模糊的量词。由于具体记数的需要，人们开始用自己的手指，伸出一个手指去说明有一只兔子或抓住一只羔羊，正整数1就这样诞生了，由1而有2、3、4……；为了表示更多的数，人们借助于用具来体现，由于用具选择的不同，体现的规则也不尽相同，从而形成不同的位值数，如：我国以手指记数，指头至十完结，十之后借助于绳子打结，形成“结绳记数”的十进制规则，后逐渐以“结绳”与手指共同记数，成为世界上最早采用十进制的国家；古希腊则“以石记数”，沿用古巴比伦的六十进位制；而中美洲的马雅人采用二十进位制，等。

现在国际上记数符号――数字，为阿拉伯数字，实质是文字诞生较早的印度首先发明和使用的，后传入阿拉伯，十三世纪才由欧洲人将之译成拉丁文而传入欧洲。所以，在欧洲人看来，数字来自阿拉伯而称阿拉伯数字，但在译制过程中，不同时代随社会文明的进步，代码及符号又不尽相同。至1522年，英国的Tonstall所写的书中，才形成现在这种数字写法。

这样，加上一些运算规则，形成了正整数体系的雏形，系统的定义则是在公理化思想、集合概念都出现后，由意大利的Peano于1891年在他的论文《关于数的概念》中提出的，称自然数公理（Peano说的自然数即正整数，不含数字0），其要点是五条公理：①1是自然数；②1不是任何其他自然数的直接后继者；③每个自然数a都有一个后继者；④若a 的后继者与b的后继者相等，则a与b相等；⑤若一个自然数组成的集合S含有1，又若当S含有任意数a时，它一定含有a的后继者，则S含有全体自然数。这样，正整数才真正走到成熟。

二，分数、负数、零的引入，使数在纤纤细步的增容中完成量变的积累

3、p=1/8

备课资料：

        数系的发展历程

数的概念是从生活、生产、科研等社会实践中发展起来的，每一种数的发展均有两个方向：一是其内涵的增容、规范及应用的日臻完善的纵向过程，二是对其出现的不可调和的矛盾而衍生新数的横向发展，在这种纵横交错中，数一步步走向系统完整。

一，正整数在勇往直前中成熟

2、(4,)

1、kπ+,k∈Z

3、关于x的方程x²-(2i-1)x+2p-i=0有实数根，求实数p的值或范围

[答案]

2、设z=log₂(m²-3m-3)+ilog₂(m-3),若其实部的范围是(0,1)，则实数m的范围是___________

1、复数z=sin2x-i(1-cos2x)是纯虚数，则实数x=____________

（2）、复数的代数形式：；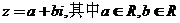

（2）、复数的有关概念：虚数，纯虚数，实部、虚部、复数相等。

[补充习题]