
(2)d>0, <
<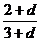
解答:(1)d>0, <
<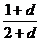
(2)  <
< ,
, <
< ,
, <
< ,......由此归纳出一般结论
,......由此归纳出一般结论
(3)由(1)和(2),归纳出一个更一般的结论,并证明
例3、(1) <
< ,
,  <
< ,
, <
< ,
, <
< ,…………,由此归纳出一般结论
,…………,由此归纳出一般结论
例2、自然数的平方的末位数字能否为2?
解答:自然数平方的末位数字取决于自然数的末位数字,一个自然数的末位数字可以是0,1,2,3,4,5,6,7,8,9十种情况,于是有
N的末位数字
0
1
2
3
4
5
6
7
8
9
N2的末位数字
0
1
4
9
6
5
6
9
4
1
末位数字不可能是2
说明:这种将所有情况列举出的归纳推理称完全归纳法,它适用于有限的情况,结论一定正确。相应的没有说明所有情况的归纳推理称不完全归纳法
练习:数列{an}满足 ,猜测an=_________________(
,猜测an=_________________( )
)
例1、三角形的内角和是1800,凸四边形的内角和是3600,凸五边形的内角和是5400,凸六边形的内角和是7200, ……,由此归纳:凸n边形的内角和是_______________((n-2)1800)
说明1:归纳推理的过程是:实验观察→概括推广→猜测一般结论
|