1、平行六面体的体对角线交于一点且互相平分

4、平面内，若射线OM、ON上分别存在点M₁、M₂与点N₁、N₂，则三角形面积比=；类比到空间，若不在同一平面的射线OP、OQ、OQ上分别存在点P₁和P₂,Q₁和Q₂，R₁和R₂，则体积比=______________

[答案]

3、平面直角坐标系xOy中，A、B不全为0，则Ax+By+C=0表示一条直线方程，且(A,B)为该直线的一个法向量，点(x₀,y₀)到直线的距离为，写出空间一个类似的结论

2、在公差为d(d≠0)的等差数列{a_n}中，S_n是{a_n}的前n项和，则数列S₂₀-S₁₀,S₃₀-S₂₀,S₄₀-S₃₀也成等差数列，且公差为100d；类比此结论，对于公比为q的等比数列{b_n}的前n项积为T_n,则满足______________

1、平行四边形对角线交于一点且互相平分，类比到空间有_______________

解：四面体内切球半径为R，四个面的面积分别为S₁,S₂,S₃,S₃,则四面体的体积为V=R(S₁+S₂+S₃+S₄)

练习：教材P67---练习题

[补充习题]

例、三角形内切圆半径为r，三边长为a,b,c，则三角形的面积V=r(a+b+c)，写出空间一个类似结论。

汇总2：类比推理结果未必正确，也属于一种合情推理。这样合情推理中最常见的两种推理就是归纳与类比，前者是由特殊到一般，后者是由特殊到特殊

汇总3：类比推理的过程：观察比较→联想类推→猜测新结论

2、鲁班通过被刺菜发明了锯，这一推理过程是归纳推理吗？实质是什么？（不是归纳推理，是由特殊到特殊的推理，将这种推理命名为类比推理）

汇总1：类比推理的一般模式是

4、n²,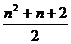

                            第二课时   类比推理

[教学目标]

[教学重点]类比推理

[教学难点]类比推理的正确性

[教学过程]