
昆十四中2009届高三年级统测
理 科 数 学
时间:120分钟 满分:150分
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数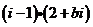 是纯虚数,则实数
是纯虚数,则实数 等于( )
等于( )
A.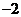 B.
B. C.
C.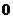 D.
D.
2.直线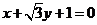 的倾斜角是( )
的倾斜角是( )
A.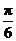 B.
B.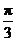 C.
C. D.
D.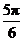
3.某中学有高一、高二、高三学生共 名,其中高三学生
名,其中高三学生 名,如果用分层抽样的方法从这
名,如果用分层抽样的方法从这 人抽取一个
人抽取一个 人的样本,那么应当从高三学生中抽取的人数是( )
人的样本,那么应当从高三学生中抽取的人数是( )
A.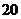 B.
B. C.
C. D.
D.
4.函数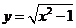
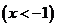 的反函数是( )
的反函数是( )
A.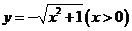 B.
B.
C. D.
D.
5.已知函数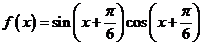 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.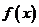 的最小正周期为
的最小正周期为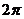 ,其图象的一条对称轴为
,其图象的一条对称轴为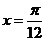
B.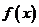 的最小正周期为
的最小正周期为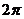 ,其图象的一条对称轴为
,其图象的一条对称轴为
C.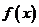 的最小正周期为
的最小正周期为 ,其图象的一条对称轴为
,其图象的一条对称轴为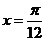
D.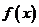 的最小正周期为
的最小正周期为 ,其图象的一条对称轴为
,其图象的一条对称轴为
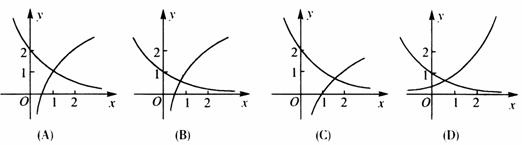
6.函数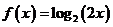 与
与 在同一直角坐标系下的图象是( )
在同一直角坐标系下的图象是( )
7.设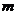 、
、 、
、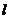 是三条不同的直线,
是三条不同的直线,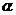 、
、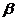 、
、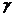 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )
A.若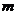 ,
, 与
与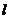 所成的角相等,则
所成的角相等,则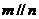
B.若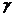 与
与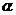 ,
,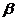 所成的角相等,则
所成的角相等,则
C.若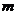 ,
, 与
与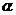 所成的角相等,则
所成的角相等,则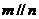
D.若 ,
,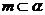 ,则
,则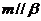
8.若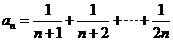
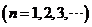 ,则
,则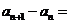 ( )
( )
A.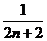 B.
B.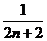
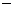
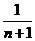 C.
C.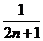
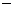
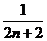 D.
D.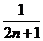

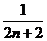
9.某电视台连续播放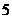 个不同的广告,其中有
个不同的广告,其中有 个不同的商业广告和
个不同的商业广告和 个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且两个奥运宣传广告不能连续播放,则不同的播放方式有( )
个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且两个奥运宣传广告不能连续播放,则不同的播放方式有( )
A. 种 B.
种 B.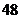 种 C.
种 C. 种 D.
种 D.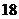 种
种
10.已知P、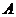 、
、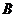 、
、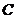 是平面内四点,且
是平面内四点,且 ,那么一定有( )
,那么一定有( )
A. B.
B. C.
C.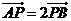 D.
D.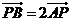
11.已知元素为实数的集合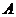 满足条件:若
满足条件:若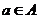 ,则
,则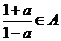 ,那么集合
,那么集合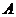 中所有元素的乘积
中所有元素的乘积
为( )
A.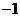 B.
B. C.
C.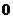 D.
D.
12.双曲线 的左、右焦点分别为
的左、右焦点分别为 、
、 ,点
,点
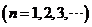 在其右支上,且满足
在其右支上,且满足 ,
,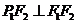 ,则
,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
二、填空题:本大题共4小题,每小题5分,共20分。把答案直接答在答题卡上
13.已知映射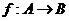 ,集合
,集合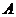 中元素
中元素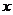 在对应法则
在对应法则 作用下的象为
作用下的象为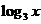 ,那么
,那么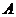 中元素
中元素 的象
的象
是
14.设圆 关于直线
关于直线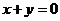 对称的圆为
对称的圆为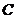 ,则圆
,则圆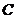 的圆心坐标为
,
的圆心坐标为
,
再把圆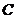 沿向量
沿向量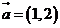 平移得到圆
平移得到圆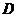 ,则圆
,则圆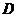 的方程为
的方程为
15.若 ,则
,则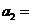 ,
,
16.在棱长为 的正方体
的正方体 中,
中, 、
、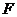 分别为棱
分别为棱 和
和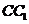 的中点,则线段
的中点,则线段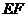 被正方体的内切球球面截在球内的线段长为
被正方体的内切球球面截在球内的线段长为
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤
17、(本小题满分10分)
在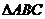 中,已知
中,已知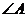 为锐角,且
为锐角,且
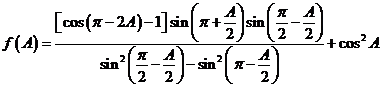
(Ⅰ)求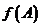 的最大值;
的最大值;
(Ⅱ)若 ,
, ,
,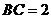 ,求
,求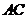 边的长。
边的长。
18、(本小题满分12分)
某单位为普及奥运知识,根据问题的难易程度举办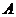 、
、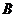 两种形式的知识竞猜活动。
两种形式的知识竞猜活动。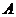 种竞猜活动规定:参赛者回答
种竞猜活动规定:参赛者回答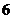 个问题后,统计结果,答对
个问题后,统计结果,答对 个,可获福娃一个;答对
个,可获福娃一个;答对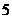 个或
个或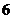 个,可获其它奖品;
个,可获其它奖品;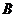 种竞猜活动规定:参赛者依次回答问题,答对一个问题就结束竞猜,且最多回答
种竞猜活动规定:参赛者依次回答问题,答对一个问题就结束竞猜,且最多回答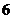 个问题,答对一个问题者可获福娃一个。假定参赛者答对每个问题的概率均为
个问题,答对一个问题者可获福娃一个。假定参赛者答对每个问题的概率均为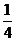
(Ⅰ)求某人参加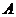 种竞猜活动只获得一个福娃奖品的概率;
种竞猜活动只获得一个福娃奖品的概率;
(Ⅱ)设某人参加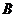 种竞猜活动,结束时答题数为
种竞猜活动,结束时答题数为 ,求
,求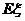
 19、(本小题满分12分)
19、(本小题满分12分)
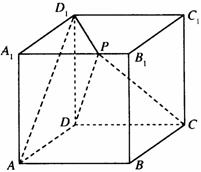
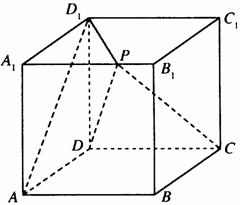
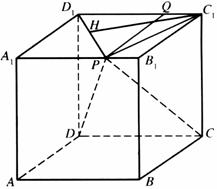
如图,正方体 的棱长为
的棱长为 ,动点
,动点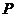 在棱
在棱 上
上
(Ⅰ)求证: ;
;
(Ⅱ)当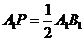 时,求
时,求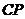 与平面
与平面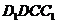 所成角的正弦值;
所成角的正弦值;
(Ⅲ)当 时,求点
时,求点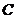 到平面
到平面 的距离。
的距离。
20、(本小题满分12分)
已知抛物线的方程为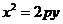
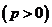 ,过点
,过点 的直线
的直线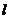 与抛物线相交于
与抛物线相交于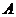 、
、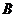 两点,分别过点
两点,分别过点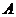 、
、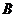 作抛物线的两条切线
作抛物线的两条切线 和
和 ,记
,记 和
和 相交于点
相交于点
(Ⅰ)证明:直线 和
和 的斜率之积为定值;
的斜率之积为定值;
(Ⅱ)求点M的轨迹方程。
21、(本小题满分12分)
已知数列 为等差数列.
为等差数列.
(Ⅰ)若 ,公差
,公差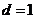 ,且
,且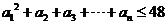 ,求
,求 的最大值;
的最大值;
(Ⅱ)对于给定的正整数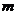 ,若
,若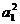

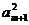
 ,求
,求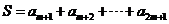 的最大值
的最大值
22、(本小题满分12分)
已知函数
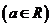
(Ⅰ)若函数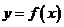 的图象在点
的图象在点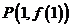 处的切线的倾斜角为
处的切线的倾斜角为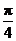 ,求
,求 ;
;
(Ⅱ)设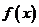 的导函数是
的导函数是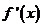 ,在(Ⅰ)的条件下,若
,在(Ⅰ)的条件下,若 ,求
,求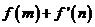 的最小值;
的最小值;
(Ⅲ)若存在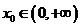 ,使
,使 ,求
,求 的取值范围。
的取值范围。
![]() 昆十四中2008届高三年级适应性考试
昆十四中2008届高三年级适应性考试
理科数学 答题卡
 满分:
满分: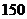 分 时间:
分 时间: 分钟
得分
分钟
得分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每小题5分,共20分)
13. 14.
15. 16.
三、解答题(共70分)
17.(本小题满分10分)
18.(本小题满分12分)
19.(本小题满分12分)
20. (本小题满分12分)
21. (本小题满分12分)
22. (本小题满分12分)
![]() 昆十四中2009届高三年级统测
昆十四中2009届高三年级统测
理科数学 答案
 满分:
满分: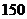 分 时间:
分 时间: 分钟
得分
分钟
得分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
A
C
A
D
C
C
D
B
C
二、填空题(每小题5分,共20分)
13. 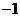 14.
14. 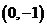 ,
, 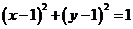
15.  ,
, 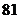 16.
16. 
三、解答题(共70分)
17.(本小题满分10分)
解:(1)

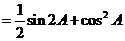
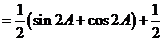
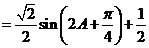
因为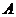 为锐角 ,所以
为锐角 ,所以 ,
,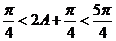
 当
当 时,
时,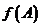 取得最大值,其最大值为
取得最大值,其最大值为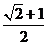
(2)由 ,得
,得 ,得
,得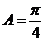
又

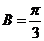
在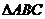 中,由正弦定理得
中,由正弦定理得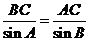

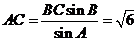
18.(本小题满分12分)
解:(Ⅰ)设事件“某人参加A种竞猜活动只获得一个福娃奖品”为事件M,依题意,答对一题的概率为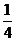 ,则
,则
P(M)=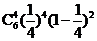 =15×
=15× =
=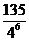 =
=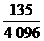 .
.
(Ⅱ)依题意,某人参加B种竞猜活动,结束时答题数 =1,2,…,6,
=1,2,…,6,
则P( =1)=
=1)=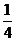 ,P(
,P( =2)=
=2)= ,P(
,P( =3)=
=3)= ,P(
,P( =4)=
=4)= , P(
, P( =5)=
=5)= ,
,
P( =6)=
=6)= 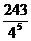 ,
,
所以,  的分布列是
的分布列是

1
2
3
4
5
6
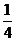




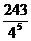
E =1×
=1×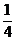 +2×
+2×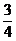 ×
×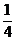 +…+5×
+…+5× ×
×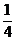 +6×
+6× .
.
设S=1+2×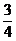 +…+5×
+…+5× ,
,
则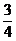 S=
S=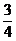 +2×
+2×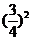 +3×
+3×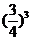 +4×
+4× +5×
+5× ,
,
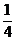 S=1+
S=1+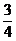 +
+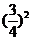 +
+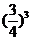 +
+ -5×
-5× =
=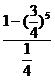 -5×
-5× ,
,
E =
=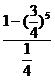 -5×
-5× +6×
+6× =
= =
= .
.
答:某人参加A种竞猜活动只获得一个福娃奖品的概率为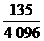 ;某人参加B种竞猜活动,
;某人参加B种竞猜活动,
结束时答题数为 ,E
,E 为
为 .
.
19.(本小题满分12分)
解法一:(Ⅰ)证明:连结A1D,在正方体AC1中,∵A1B1⊥平面A1ADD1,
∴A1D是PD在平面A1ADD1内的射影.
∵在正方形A1ADD1中,A1D⊥AD1,∴PD⊥AD1.
解:(Ⅱ)取D
∵A1D1⊥平面D1DCC1,∴PM⊥平面D1DCC1.
∴CM为CP在平面D1DCC1内的射影.则∠PCM为CP与平面D1DCC1
所成的角.
在Rt△PCM中,sinPCM=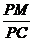 =
=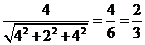 .
.
∴CP与平面D1DCC1所成角的正弦值为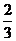 .
.
 (Ⅲ)在正方体AC1中,D1D∥C
(Ⅲ)在正方体AC1中,D1D∥C
∵C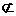 平面D1DP内,
平面D1DP内,
∴C
∴点C到平面D1DP的距离与点C1
到平面D1DP的距离相等.
又D1D⊥平面A1B
DD1 平面D1DP
平面D1DP
∴平面D1DP⊥平面A1B
又平面D1DP∩平面A1B
D1P,过C1作C1H⊥D1P于H,
则C1H⊥平面D1DP.
∴C1H的长为点C1到平面D1DP的距离.
连结C1P,并在D
C1H?D1P=PQ?D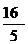 .
.
∴点C到平面D1DP的距离为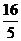 .
.
解法二:如图,以D为坐标原点,建立空
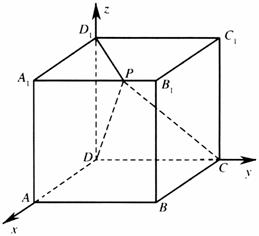 间直角坐标系D-xyz.
间直角坐标系D-xyz.
由题设知正方体棱长为4,则
D(0,0,0) ,A(4,0,0),
B1(4,4,4) ,A1(4,0,4),
D1(0,0,4) ,C(0,4,0).
(Ⅰ)设P(4,y0,4),
∴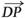 =(4,y0,4),
=(4,y0,4),
∴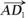 =(-4,0,4)
=(-4,0,4)
∵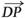 ?
?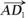 =-16+16=0,
=-16+16=0,
∴PD⊥AD1.
(Ⅱ)由题设可得,P(4,2,4),故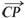 =(4,-2,4).
=(4,-2,4).
∵AD⊥平面D1DCC1, ∴ =(4,0,0)是平面D1DCC1的法向量.
=(4,0,0)是平面D1DCC1的法向量.
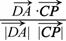 ∴cos<
∴cos< ,
,
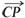 >=
=
>=
=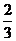 .
.
∴CP与平面D1DCC1所成角的正弦值为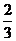 .
.
(Ⅲ) ∵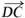 =(0,4,0),设平面D1DP的法向量n=(x,y,z),
=(0,4,0),设平面D1DP的法向量n=(x,y,z),
∵P(4,3,4), ∴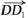 =(0,0,4),
=(0,0,4),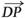 =(4,3,4).
=(4,3,4).
 则
即
则
即 令x=-3,则y=4.
令x=-3,则y=4.
∴n=(-3,4,0).
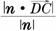 ∴点C到平面D1DP的距离为d= =
∴点C到平面D1DP的距离为d= =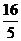 .
.
20. (本小题满分12分)
(Ⅰ)解:依题意,直线l的斜率存在,设直线l的方程为y=kx+p,
将其代入x2=2py,消去y整理得x2-2pkx-2p2=0.
设A,B的坐标分别为A(x1,y1),B(x2,y2),则x1x2=-2p2.
将抛物线的方程改写为y=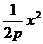 ,求导得y′=
,求导得y′=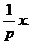
所以过点A的切线l1的斜率是k1=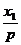 ,过点B的切线l2的斜率是k2=
,过点B的切线l2的斜率是k2=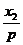 ,
,
故k1k2=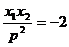 ,所以直线l1和l2的斜率之积为定值-2.
,所以直线l1和l2的斜率之积为定值-2.
(Ⅱ)【法一】解:
设M(x,y).因为直线l1的方程为y-y1=k1(x-x1),即 ,
,
同理,直线l2的方程为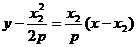 ,
,
联立这两个方程,消去y得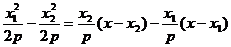 ,
,
整理得(x1-x2)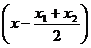 =0,注意到x1≠x2,所以x=
=0,注意到x1≠x2,所以x= .
.
此时y=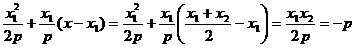 .
.
由(Ⅰ)知,x1+x2=2pk,所以x= =pk
=pk R,
R,
所以点M的轨迹方程是y=-p.
【法二】设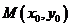 ,则直线
,则直线 的方程为
的方程为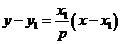 即
即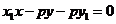
因点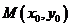 在直线
在直线 上 故
上 故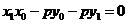
于是点 在直线
在直线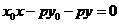 上
上
同理,点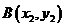 在直线
在直线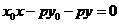 上
上
 直线
直线 的方程为
的方程为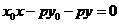
又直线 经过点
经过点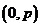

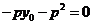

即点 的轨迹为
的轨迹为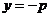
21. (本小题满分12分)
(I)解:由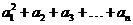 ≤48,
≤48,
可得 ≤48,又a1=3,d=1,
≤48,又a1=3,d=1,
可得6+3n+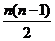 ≤48.
≤48.
整理得 n2+5n-84≤0,
解得-12≤n≤7,
即n的最大值为7.
(II)解:S=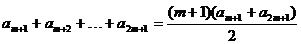 ,
,
设am+1+a
则A=am+1+ a
则am+1=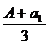 ,
,
由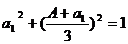 ,
,
可得
由△=
可得-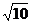 ≤A≤
≤A≤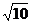 .
.
所以S= ≤
≤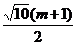 .
.
即S的最大值为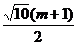 .
.
22. (本小题满分12分)
解:(Ⅰ)f′(x)=-3x2+2ax.
据题意,f′(1)=tan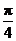 =1, ∴-3+
=1, ∴-3+
(Ⅱ)由(Ⅰ)知f(x)=-x3+2x2-4,
则f′(x)=-3x2+4x.
X
-1
(-1,0)
0
(0,1)
1
f′(x)
-7
-
0
+
1
f(x)
-1
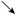
-4
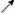
-3
∴对于m [-1,1],f(m)的最小值为f(0)=-4
[-1,1],f(m)的最小值为f(0)=-4
∵f′( x)=-3x2+4x的对称轴为x=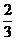 ,且抛物线开口向下,
,且抛物线开口向下,
∴x [-1,1]时,f′( x)的最小值为f′( -1)与f′( 1)中较小的.
[-1,1]时,f′( x)的最小值为f′( -1)与f′( 1)中较小的.
∵f′( 1)=1,f′( -1)=-7,
∴当x [-1,1]时,f′( x)的最小值为-7.
[-1,1]时,f′( x)的最小值为-7.
∴当n [-1,1]时,f′ ( x)的最小值为-7.
[-1,1]时,f′ ( x)的最小值为-7.
∴f(m)+ f′( n)的最小值为-11.
(Ⅲ) ∵f′( x)= -3x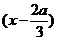 .
.
①若a≤0,当x>0时,f′( x)<0, ∴f(x)在[0,+∞ 上单调递减.
上单调递减.
又f(0)=-4,则当x>0时,f(x)<-4.
∴当a≤0时,不存在x0>0,使f(x0)>0.
②若a>0,则当0<x<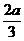 时,f ′( x)>0,当x>
时,f ′( x)>0,当x>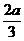 时,f ′( x)<0.
时,f ′( x)<0.
从而f(x)在(0, 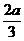
 上单调递增,在 [
上单调递增,在 [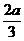 ,+∞
,+∞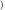 上单调递减.
上单调递减.
∴当x (0,+∞)时,
f(x)max=f(
(0,+∞)时,
f(x)max=f(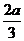 )=-
)=-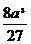 +
+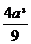 -4=
-4= -4.
-4.
据题意, -4>0,即a3>27.
∴a>3.
-4>0,即a3>27.
∴a>3.
综上,a的取值范围是(3,+∞).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com