
题目列表(包括答案和解析)
20.三人独立破译同一份密码.已知三人各自破译出密码的概率分别为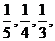 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
19.有4名老师和4名学生一起照相。
(I)全部站成一排,共有多少种不同的排法?
(II)全部站成一排,4名学生必须排在一起,共有多少种不同的排法?
(III)全部站成一排,任两名学生都不能相邻,共有多少种不同的排法?
(要求用数字作答)
18. 从0,1,2,3,4,5,6这7个数中4个数组成无重复数字的四位数,并把它们按从小到大的顺序排列,则3245是第 ------ 个数(用数字作答)。
17. 盒中有5个红球,11个蓝球。红球中有2个玻璃球,3个木质球;蓝球中有4个玻璃球,7个木质球。现从中任取一球,假设每个球摸到的可能性都相同,若已知取到的球是玻璃球,则它是蓝球的概率是-------
16. 用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是 (用数字作答)。
15.若(2x+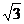 )4=a0+a1x+a2x2+a3x3+a4x4,
则(a0+a2+a4)2-(a1+a3)2 的值为______________________
)4=a0+a1x+a2x2+a3x3+a4x4,
则(a0+a2+a4)2-(a1+a3)2 的值为______________________
14. 若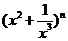 展开式的各项系数之和为32,则n= ,其展开式中的常数项为 。(用数字作答)
展开式的各项系数之和为32,则n= ,其展开式中的常数项为 。(用数字作答)
13. 在(x-a)10的展开式中,x7的系数是15,则实数a=_____
18.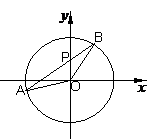 由点P(0,1)引圆
由点P(0,1)引圆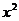 +
+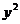 =4的割线
=4的割线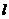 ,交圆于A,B两点,使ΔAOB的面积为
,交圆于A,B两点,使ΔAOB的面积为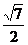 (O为原点),求直线
(O为原点),求直线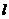 的方程.
的方程.
解:直线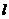 的方程为:
的方程为: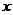 -
-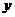 +1=0或
+1=0或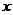 +
+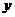 -1=0.
-1=0.
17.已知圆C和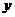 轴相切,圆心C在直线
轴相切,圆心C在直线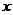 -3
-3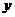 =0上,且被直线
=0上,且被直线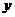 =
=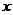 截得的弦长为
截得的弦长为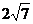 ,求圆C的方程.
,求圆C的方程.
解:设圆心坐标为(3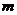 ,
,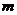 ).因为圆C和
).因为圆C和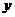 轴相切,得圆的半径为3|
轴相切,得圆的半径为3|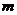 |,
|,
所以圆心到直线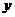 =
=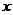 的距离为
的距离为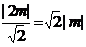 .
.
由半径、弦心距、半径的关系得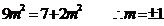
∴所求圆的方程为: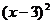 +
+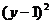 =9或
=9或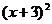 +
+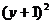 =9.
=9. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com