7．解排列组合问题的依据是：分类相加，分步相乘，有序排列，无序组合．

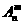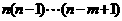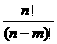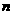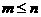(1)排列数公式 ：== (，∈N^*，且)．规定．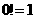

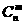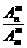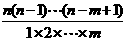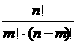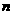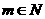(2)组合数公式：===(∈N^*，，且)．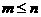

6．对立事件(事件、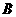不可能同时发生,但、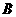中必有一个发生，两个事件为对立事件):

(1)事件的对立事件记为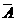：．(2) ．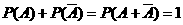

(3)当计算事件A的概率P(A)比较困难时，有时计算它的对立事件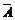的概率要容易：P(A)=1－P()

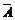(4)对立事件一定是互斥事件，但互斥事件不一定是对立事件．

5．互斥事件(、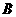互斥，即事件、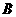不可能同时发生)

(1)一般地：如果事件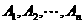中的任何两个都是互斥的，那么就说事件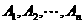彼此互斥．

若事件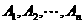彼此互斥，则＝．

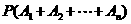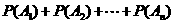(2)事件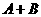(事件的和):事件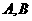至少有一个发生，表示“或” ．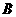

若事件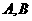互斥，则事件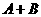发生的概率等于事件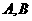分别发生的概率的和，即．

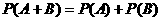注：当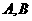为互斥事件时，事件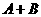是由“发生而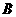不发生”以及“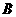发生而不发生”构成的，

因此当和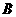互斥时，事件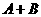的概率满足加法公式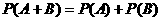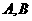： 　(互斥).

4．几何概型：如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成正比，则称这样的概率模型为几何概型．

(1)特点： ①无限性：一次试验中，可能出现的结果有无限多个．

②等可能性：每个结果的发生具有等可能性．

(2)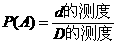．　　　　　　 (3)“测度”可以是长度、面积、体积、角度．

3．古典概型：

(1)特点： ①有限性：试验中所有可能出现的基本事件只有有限个．

　②等可能性：每个基本事件出现的可能性相等．

(2)若试验的所有基本事件数为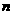，随机事件包含的基本事件数为，则事件的概率定义为[]　 即：．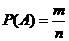

2．随机事件的概率：

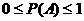(1)；　　　　　　　　 (2)当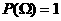时称为必然事件；当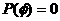时称为不可能事件．

必然事件和不可能事件看作随机事件的两个极端情形．

1．事件的概念：在一次试验中出现的试验结果，叫做事件。一般用大写字母A，B，C，…表示．

(1)必然事件：必然会发生的事件．

(2)不可能事件：肯定不会发生的事件．

(3)随机事件：可能发生也可能不发生的事件．

8．在直四棱柱ABCD－A₁B₁C₁D₁中，AB＝AD＝2，DC＝2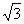，AA₁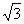＝，AD⊥DC，AC⊥BD， 垂足为E．

　 (Ⅰ)求证：BD⊥A₁C；

　 (Ⅱ)求二面角A ₁－BD－C ₁的大小；

　 (Ⅲ)求异面直线 AD与 BC ₁所成角的大小．

7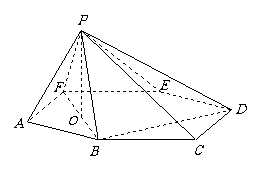．如图，P是边长为1的正六边形ABCDEF所在平面外一点，PA=1，P在平面ABC内的射影为BF的中点O ．

(Ⅰ)证明PA⊥PB；

(Ⅱ)求面APB与面DPB所成二面角的大小．

6．若正四棱锥的底面边长为2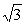cm，体积为4cm³，则它的侧面与底面所成的二面角的大小是　　　　　　　 ．