18.(15分)设关于x的一元二次方程x²+2ax+b²=0.

(1)若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率.

(2)若a是从区间［0，3］任取的一个数，b是从区间［0，2］任取的一个数，求上述方程有实根的概率.

17.(15分)袋中装有黑球和白球共7个，从中任取两个球都是白球的概率为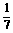.现有甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.

(1)求袋中原有白球的个数；

(2)求取球2次终止的概率；

(3)求甲取到白球的概率.

16.(14分)函数y=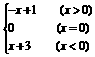,写出求该函数值的算法及流程图.

15.(14分)甲、乙两个车间分别制作一种零件，在自动包装传送带上每隔10分钟抽取一件产品，测其质量，分别记录抽查的数据如下：

甲：102， 101，　 99，　　 98，　　 103，　 98，　　 99；

乙：105， 102，　 97，　　 92，　　 96， 101，　 107；

(1)这种抽样方法是什么抽样？

(2)估计甲、乙两个车间产品质量的平均值与方差，并分析哪个车间的产品较稳定；

(3)如果产品质量在区间(95，105)内为合格，那么这个工厂生产的产品合格率是多少？

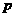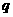14.下列各小题中，是的充分必要条件的是　　　 ▲　　　　　

①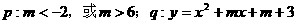有两个不同的零点

②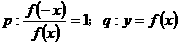是偶函数

③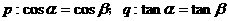

④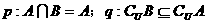

13.已知命题p:x∈R，使tanx=1,命题q：x²-3x+2＜0的解集是{x|1＜x＜2}，下列结论：　

①命题“p∧q”是真命题；　

②命题“p∧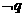”是假命题；　

③命题“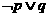”是真命题；

④命题“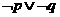”是假命题.

其中正确的是　　 ▲　　 (填序号).

12.将长为l的棒随机折成3段，则3段构成三角形的概率是　　　 ▲　　　　 .

11.在平面直角坐标系xOy中，设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域，E是到原点的距离不大于1的点构成的区域，向D中随机投一点，则落入E中的概率为　　 ▲　　 .

10.设集合A={1，2}，B={1，2，3}，分别从集合A和B中随机取一个数a和b，确定平面上的一个点P(a，b)，记“点P(a,b)落在直线x+y=n上”为事件C_n(2≤n≤5，n∈N)，若事件C_n的概率最大，则n的所有可能值为　　　 ▲　　 .

9.将一颗质地均匀的骰子(它是一种各面上分别标有点数1，2，3，4，5，6的正方体玩具)先后抛掷3次，至少出现一次6点向上的概率是　　 ▲　　 .