
题目列表(包括答案和解析)
5.已知抛物线y=ax2+bx+c与直线y=x-2相交于(m,-2),(n,3)两点,且抛物线的对称轴为直线x=3,求函数的关系式。
4.已知函数y=x2-x-2。
(1)先确定其图象的开口方向、对称轴、顶点坐标和与两坐标轴的交点,再画出图象
(2)观察图象确定:x取什么值时,①y=0,②y>0;③y<0。
3.已知抛物线y1=x2+x-k与直线y=-2x+1的交点的纵坐标为3。
(1)求抛物线的关系式;
(2)求抛物线y=x2+x-k与直线y=-2x+1的另一个交点坐标.
2. 二次函数y=x2-3x-18的图象与x轴有两交点,求两交点间的距离。
1.填空。
(1)抛物线y=x2-x-2与x轴的交点坐标是______,与y轴的交点坐标是______ .
(2)抛物线y=2x2-5x+3与y轴的交点坐标是______,与x轴的交点坐标是______ .
(3)抛物线y=x2+5x-6与y轴的交点C的坐标是______,与x轴的交点A、B坐标分别是______ ,△ABC的面积是 .
2、二次函数与一元二次不等式的关系:
如图1, ①方程ax2+bx+c=0的解是 ;
②当x满足 时,函数值大于0;
③当x满足 时,函数值小于0.
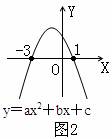
如图2, ①方程ax2+bx+c=0的解是 ;
②当x满足 时,函数值大于0;
③当x满足 时,函数值小于0.
[例题解析]
例1、已知抛物线y1=2x2-8x+k+8和直线y2=mx+1相交于点P(3,4m).
(1) 求这两个函数的关系式;
(2) 求抛物线与直线的另一交点坐标.
解:(1)∵点P(3,4m)在直线y2=mx+1上.
∴有4m=3m+1.
解得m=1
∴y1=x+1,P(3,4).
∵点P(3,4)在抛物线y1=2x2-8x+k+8上.
∴4=18-24+k+8.
解得 k=2
∴y1=2x2-8x+10.
(2)依题意,得 解这个方程组,得,
∴抛物线与直线的另一交点坐标是(1.5,2.5).
[实弹射击]
1、二次函数与一元二次方程的关系:
 (1)如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标即为方程ax2+bx+c=0的解;
(1)如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标即为方程ax2+bx+c=0的解;
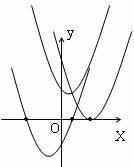
(2)如图,抛物线y=ax2+bx+c与x轴的位置关系有三种:
①没有公共点:一元二次方程ax2+bx+c=0的解的情况是 ;
②有一个公共点:一元二次方程ax2+bx+c=0的解的情况是 ;
③有两个公共点:一元二次方程ax2+bx+c=0的解的情况是 。
(3)当a>0时,抛物线y=ax2+bx+c的顶点位置与一元二次方程ax2+bx+c=0的根的关系(如右上图):
 ①方程ax2+bx+c=0有两个不等的实数根 顶点在
;
①方程ax2+bx+c=0有两个不等的实数根 顶点在
;
 ②方程ax2+bx+c=0有两个相等的实数根 顶点在
;
②方程ax2+bx+c=0有两个相等的实数根 顶点在
;
 ③方程ax2+bx+c=0没有实数根
顶点在
;
③方程ax2+bx+c=0没有实数根
顶点在
;
(4)当a<0时,抛物线y=ax2+bx+c的顶点位置与一元二次方程ax2+bx+c=0的根的关系:
 ①方程ax2+bx+c=0有两个不等的实数根 顶点在
;
①方程ax2+bx+c=0有两个不等的实数根 顶点在
;
 ②方程ax2+bx+c=0有两个相等的实数根 顶点在
;
②方程ax2+bx+c=0有两个相等的实数根 顶点在
;
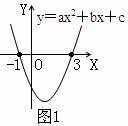
 ③方程ax2+bx+c=0没有实数根
顶点在
;
③方程ax2+bx+c=0没有实数根
顶点在
;
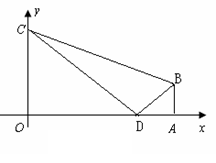
13. 如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交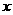 轴于E,D两点(D点在E点右方).
轴于E,D两点(D点在E点右方).
(1)求点E,D 的坐标;
(2)求过B,C,D三点的抛物线的函数关系式;
(3)过B,C,D三点的抛物线上是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.
12.某宾馆有50个房间供游客住宿,当每个房间的房价为每天l80元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的正整数倍).
(1) 设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2) 设宾馆一天的利润为w元,求w与x的函数关系式;
(3) 一天订住多少个房间时,宾馆的利润最大? 最大利润是多少元?
10. 已知二次函数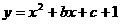 的图象过点P(2,1).
的图象过点P(2,1).
(1)求证: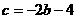 ;
;
(2)求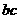 的最大值;
的最大值;
(3)若二次函数的图象与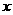 轴交于点A(
轴交于点A(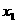 ,0)、B(
,0)、B(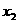 ,0),△ABP的面积是
,0),△ABP的面积是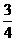 ,求
,求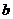 的值.
的值.
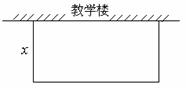
()______________________________________________________________________________________________________________________11.如图, 某中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园, 矩形的一边用教学楼的外墙,其余三边用竹篱笆. 设矩形的宽为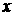 ,面积为
,面积为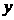 .
.
(1) 求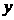 与
与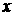 的函数关系式,并求自变量
的函数关系式,并求自变量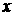 的取值范围;
的取值范围;
(2) 生物园的面积能否达到210平方米?说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com