
题目列表(包括答案和解析)
3。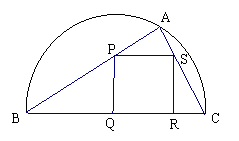 如图,某小区准备绿化一块直径为
如图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地, 外的地方种草,
外的地方种草, 的内接正方形
的内接正方形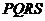 为一水池,其余地方种花.若
为一水池,其余地方种花.若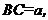
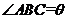 ,设
,设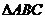 的面积为
的面积为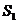 ,正方形
,正方形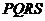 的面积为
的面积为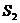 ,将比值
,将比值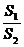 称为“规划合理度”.
称为“规划合理度”.
(1)①试用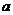 ,
,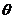 表示
表示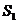 ②. 试用
②. 试用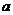 ,
,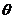 表示
表示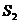
(2)当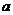 为定值,
为定值,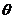 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角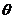 的大小.
的大小.
解:(1)、
如图,在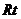
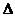 ABC中
ABC中 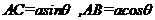 ,
,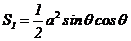 =
=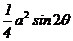
设正方形的边长为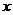 则
则 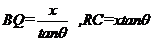
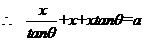
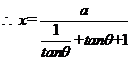 =
=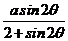
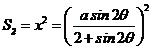 (2)、
(2)、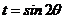 而
而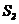 =
=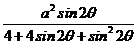
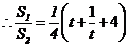 0
<
0
< 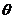 <
< 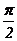 又0 <2
又0 <2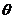 <
<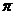 当0<
当0<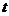 £1
£1 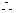
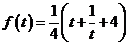 为减函数 当
为减函数 当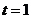 时
时 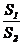 取得最小值为
取得最小值为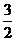 此时
此时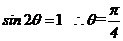
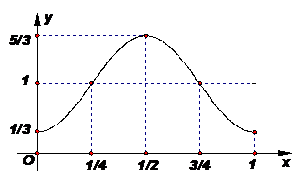
2.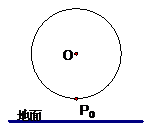 如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为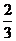 m,圆环的圆心距离地面的高度为1m,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
m,圆环的圆心距离地面的高度为1m,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度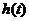 ;(2)画出函数
;(2)画出函数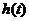 在
在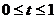 时的图象;
时的图象;
(3)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过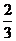 m?
m?
(1)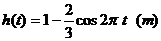 (2)图象如右实线部分(3)由
(2)图象如右实线部分(3)由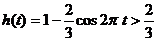 解得
解得
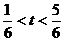 ,所以一圈内,有
,所以一圈内,有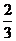 分钟的时间蚂蚁距离地面超过
分钟的时间蚂蚁距离地面超过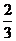 m.
m.
1.如图,在半径为R、圆心角为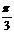 的扇形金属材料中剪出一个长方形EPQF,并且EP与
的扇形金属材料中剪出一个长方形EPQF,并且EP与 的平分线OC平行,设
的平分线OC平行,设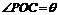 。(1)试写出用
。(1)试写出用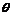 表示长方形EPQF的面积
表示长方形EPQF的面积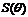 的函数。
的函数。
(2)现用EP和FQ作为母线并焊接起来,将长方形EFPQ制成圆柱的侧面,能否从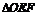 中直接剪出一个圆面作为圆柱形容器的底面?如果不能请说明理由。如果可能,求出侧面积最大时容器的体积。
中直接剪出一个圆面作为圆柱形容器的底面?如果不能请说明理由。如果可能,求出侧面积最大时容器的体积。
 (1)
(1)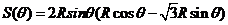 (2)依题意制成的圆柱的底面周长l=EF=
(2)依题意制成的圆柱的底面周长l=EF=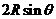 ,则其半径为
,则其半径为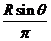 在
在 中,
中,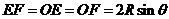
故内切圆半径r=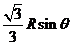 而
而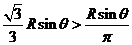 ,
,
所以能从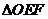 中直接剪出一个圆面作为圆柱形容器的底面。 9分
中直接剪出一个圆面作为圆柱形容器的底面。 9分
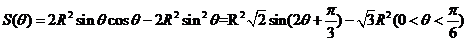
当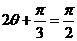 时,即
时,即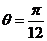 ,
,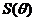 取得最大值,此时
取得最大值,此时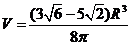 15分
15分
4. 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东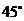 且与点A相距40
且与点A相距40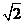 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东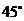 +
+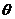 (其中sin
(其中sin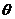 =
=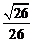 ,
,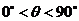 )且与点A相距10
)且与点A相距10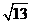 海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.解:(1)如图,AB=40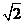 ,AC=10
,AC=10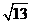 ,
, 由于
由于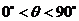 ,所以cos
,所以cos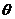 =
=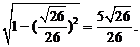 ---------4分
---------4分
由余弦定理得BC=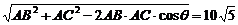
所以船的行驶速度为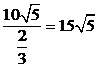 (海里/小时).------------8分
(海里/小时).------------8分
(2)解法一 以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1=
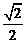 AB=40, x2=ACcos
AB=40, x2=ACcos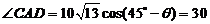 ,
,
y2=ACsin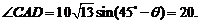 -所以过点B、C的直线l的斜率k=
-所以过点B、C的直线l的斜率k=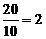 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=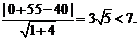 所以船会进入警戒水域.-
所以船会进入警戒水域.-
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.在△ABC中,由余弦定理得,
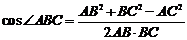 =
=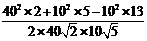 =
=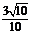 .
.
从而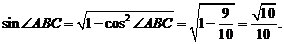 在
在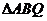 中,由正弦定理得,
中,由正弦定理得,
AQ=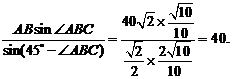 由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EP
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EP 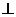 BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.
在Rt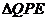 中,PE=QE·sin
中,PE=QE·sin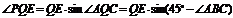 =
=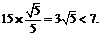 -
-
所以船会进入警戒水域.------------------------------------------------------------------------------16分
赣马高级中学解答题专题训练---三角函数05
 命题:王怀学 审核:王翔
命题:王怀学 审核:王翔
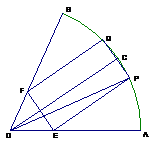
3.已知△ 的面积为3,且
的面积为3,且 。
。
(1)求 的取值范围; (2)求函数
的取值范围; (2)求函数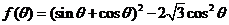 的最大值和最小值。
的最大值和最小值。
(1)设△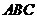 中角A,B,C的对边分别是a,b,c, 则
中角A,B,C的对边分别是a,b,c, 则
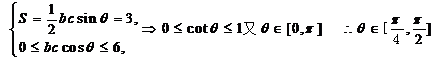
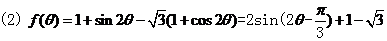
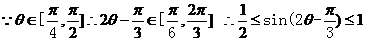
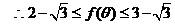
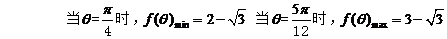
2.在 中,已知内角
中,已知内角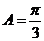 ,边
,边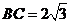 .设内角
.设内角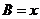 ,面积为
,面积为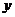 .
.
(1)求函数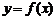 的解析式和定义域;(2)求
的解析式和定义域;(2)求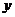 的最大值.
的最大值.
解:(1)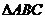 的内角和
的内角和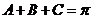
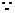
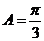
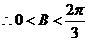
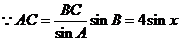
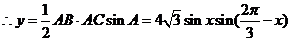
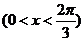
(2)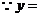
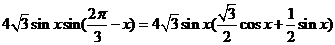
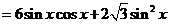
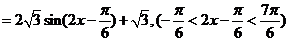
当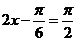 即
即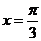 时,y取得最大值
时,y取得最大值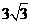 ………………………14分
………………………14分
1.在△ABC中,角A、B、C所对边分别为a,b,c,已知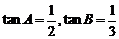 ,且最长边的边长为l.求:
,且最长边的边长为l.求:
(I)角C的大小;(II)△ABC最短边的长.
解:(I)tanC=tan[π-(A+B)]=-tan(A+B)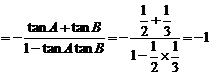
∵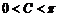 , ∴
, ∴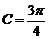 ……………………5分
……………………5分
(II)∵0<tanB<tanA,∴A、B均为锐角, 则B<A,又C为钝角,∴最短边为b ,最长边长为c
由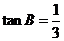 ,解得
,解得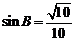 由
由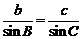 ,∴
,∴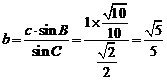
5.已知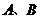 是△
是△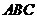 的两个内角,向量
的两个内角,向量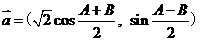 ,若
,若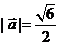 .
.
(Ⅰ)试问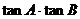 是否为定值?若为定值,请求出;否则请说明理由;
是否为定值?若为定值,请求出;否则请说明理由;
(Ⅱ)求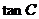 的最大值,并判断此时三角形的形状.
的最大值,并判断此时三角形的形状.
解:(Ⅰ)由条件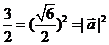
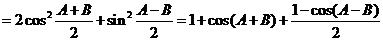
∴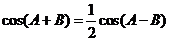 ∴
∴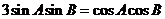 ∴
∴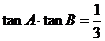 为定值.
为定值.
(Ⅱ)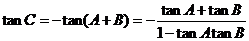 ………………………………………(7分)
………………………………………(7分)
由(Ⅰ)知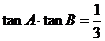 ,∴
,∴ ………………………………(8分)
………………………………(8分)
从而 ≤
≤ ………………(10分)
………………(10分)
∴取等号条件是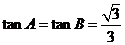 , 即
, 即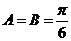 取得最大值,
取得最大值,
∴此时ΔABC为等腰钝角三角形
赣马高级中学解答题专题训练---三角函数04
命题:王怀学 审核:王翔
4.已知向量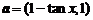 ,
,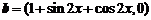 ,记
,记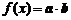 .
.
(1)求f(x)的解析式并指出它的定义域;(2)若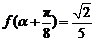 ,且
,且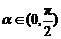 ,求
,求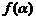 .
.
答案:(1)∵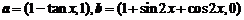 ,
,
∴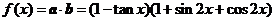
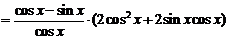
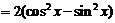
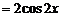 .定义域为
.定义域为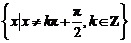 .
.
(2)因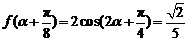 ,即
,即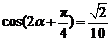 >0,
>0,
故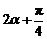 为锐角,于是
为锐角,于是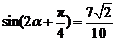 . ∴
. ∴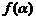 =
=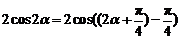
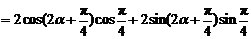 =
=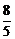 . ………………………………12分
. ………………………………12分
3.已知函数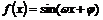 (
(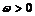 ,
,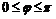 )为偶函数,且其图像上相邻的一个最高点和最低点之间距离为
)为偶函数,且其图像上相邻的一个最高点和最低点之间距离为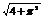 .⑴求
.⑴求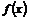 的解析式;⑵若
的解析式;⑵若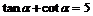 ,求
,求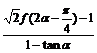 的值。
的值。
解:⑴设最高点为 ,相邻的最低点为
,相邻的最低点为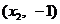 ,则|x1–x2|=
,则|x1–x2|=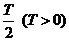
∴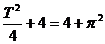 ,∴
,∴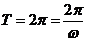 ,∴
,∴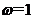 ………………………(3分)
………………………(3分)
∴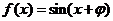 , ∵
, ∵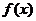 是偶函数,∴
是偶函数,∴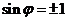 ,
,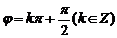 .
.
∵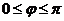 ,∴
,∴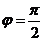 ,∴
,∴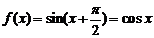 …………… (6分)
…………… (6分)
⑵∵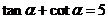 ,∴
,∴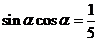 ………………………………(8分)
………………………………(8分)
∴原式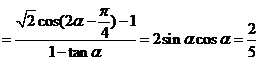
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com