
题目列表(包括答案和解析)
2、证明:(Ⅰ)由三视图可知该多面体是侧棱为a底面为等腰三角形的直三棱柱,AC=BC=a,
∠ACB=90°; 连接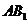 、
、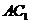 , 由平行四边形的性质可知
, 由平行四边形的性质可知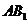 与
与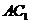 相交于点M .
相交于点M .
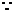 M、N分别是
M、N分别是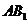 、
、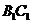 的中点,
的中点, 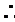
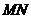 ∥
∥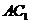
又 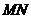
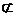 平面ACC1A1
平面ACC1A1
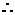 MN//平面ACC1A1
MN//平面ACC1A1
(Ⅱ)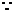
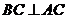
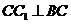
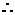
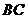 ⊥平面ACC1A1
⊥平面ACC1A1 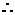
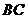 ⊥
⊥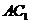 由正方形ACC1A1 性质可知
由正方形ACC1A1 性质可知
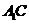 ⊥
⊥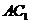
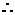
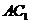 ⊥平面A1BC 又
⊥平面A1BC 又 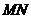 ∥
∥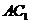 MN⊥平面A1BC
MN⊥平面A1BC
1、情况1:(1)如图(1) (2)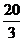 (3)
(3)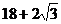
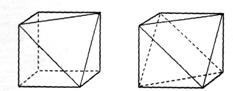
|
情况2:(1)如图(2) (2)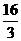 (3)
(3)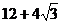
6.如图,设动点P在棱长为1的正方体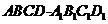 的对角线
的对角线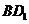 上,记
上,记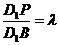 .
.
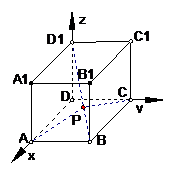 当
当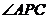 为钝角时,求
为钝角时,求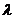 的取值范围.
的取值范围.
赣马高级中学解答题专题训练--------立体几何01答案
5.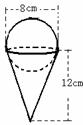 一个圆锥形的空纸杯上面抹着一个球形的冰淇淋,尺寸如图,如果冰淇淋融化了,会溢出杯子吗?说明理由
一个圆锥形的空纸杯上面抹着一个球形的冰淇淋,尺寸如图,如果冰淇淋融化了,会溢出杯子吗?说明理由
4.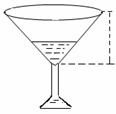 如图所示,有一圆锥形酒杯,其底面半径等于酒杯圆锥体的高,若以9
如图所示,有一圆锥形酒杯,其底面半径等于酒杯圆锥体的高,若以9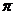 cm3/s的速度向该酒杯倒酒,则酒深10cm时酒面上升的速度为
cm3/s的速度向该酒杯倒酒,则酒深10cm时酒面上升的速度为
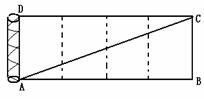
3.有一根长为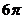 ,底面半径为1的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,使铁丝两端落在同一条母线的两端,则铁丝的长度最少为
,底面半径为1的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,使铁丝两端落在同一条母线的两端,则铁丝的长度最少为
2.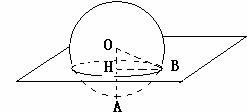 湖面上漂浮着一个丢弃的蓝球,当湖面结冰后将球取出,冰面上留下一个直径为24,深为8的球坑,则该蓝球的体积。
湖面上漂浮着一个丢弃的蓝球,当湖面结冰后将球取出,冰面上留下一个直径为24,深为8的球坑,则该蓝球的体积。
1.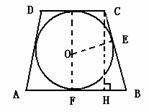 某球的外切圆台上下底面半径分别为
某球的外切圆台上下底面半径分别为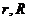 ,求该球的体积
,求该球的体积
4.在直三棱柱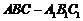 中,
中,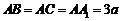 ,
,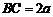 ,
,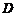 是
是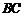 的
的 中点,
中点,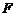 是
是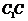 上一点,且
上一点,且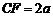 .(1)求证:
.(1)求证: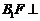 平面
平面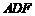 ;(2)求三棱锥
;(2)求三棱锥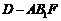 的体积;(3)试在
的体积;(3)试在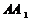 上找一点
上找一点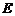 ,使得
,使得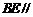 平面
平面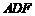 .
.
赣马高级中学解答题专题训练18--------立体几何04
命题:樊继强 审核:刘卫兵 王怀学
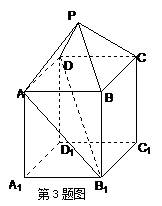
3.如图,在组合体中,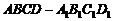 是一个长方体,
是一个长方体,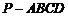 是一个四棱锥.
是一个四棱锥.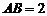 ,
,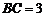 ,点
,点 且
且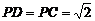 .
.
 (Ⅰ)证明:
(Ⅰ)证明: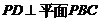 ;
;
(Ⅱ)若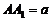 ,当
,当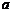 为何值时,
为何值时,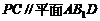 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com