
题目列表(包括答案和解析)
2.已知向量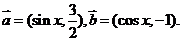 (1)当
(1)当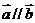 时,求
时,求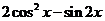 的值;(2)求
的值;(2)求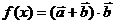 在
在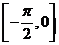 上的值域.
上的值域.
解:(1)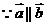 ,∴
,∴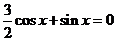 ,∴
,∴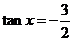
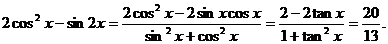 (5分)
(5分)
(2)
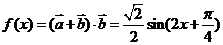
∵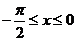 ,∴
,∴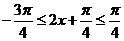 ,∴
,∴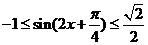
∴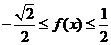 ∴函数
∴函数 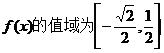
1.设函数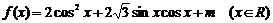
(Ⅰ)化简函数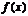 的表达式,并求函数
的表达式,并求函数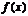 的最小正周期;
的最小正周期;
(Ⅱ)若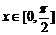 ,是否存在实数m,使函数
,是否存在实数m,使函数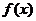 的值域恰为
的值域恰为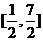 ?若存在,请求出m的取值;若不存在,请说明理由。
?若存在,请求出m的取值;若不存在,请说明理由。
解:(Ⅰ)∵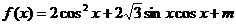
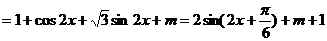 ∴函数
∴函数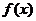 的最小正周期
的最小正周期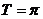
(Ⅱ)假设存在实数m符合题意, 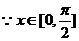 ,∴
,∴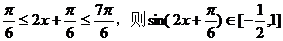 ∴
∴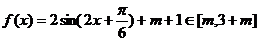 又∵
又∵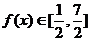 ,解得
,解得 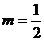
∴存在实数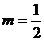 ,使函数
,使函数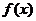 的值域恰为
的值域恰为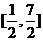
5.在△ABC中,已知角A为锐角,且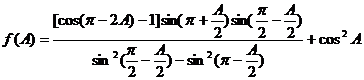 .
.
(I)求f (A)的最大值;
(II)若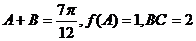 ,求△ABC的三个内角和AC边的长.
,求△ABC的三个内角和AC边的长.
解:(I)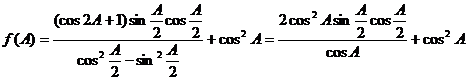
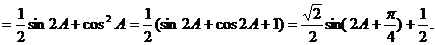 …………3分
…………3分
∵角A为锐角,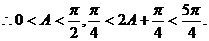 …………………………………4分
…………………………………4分
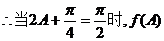 取值最大值,其最大值为
取值最大值,其最大值为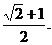 ……………………6分
……………………6分
(II)由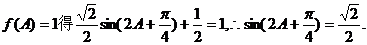 ………………8分
………………8分
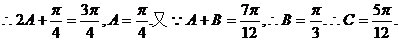 ………………10分
………………10分
在△ABC中,由正弦定理得: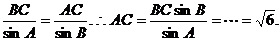
赣马高级中学解答题专题训练---三角函数03
命题:王怀学 审核:王翔
4.已知向量a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),α∈(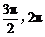 ),且a⊥b.
),且a⊥b.
(1)求tanα的值; (2)求cos(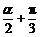 )的值.
)的值.
解:(1)∵a⊥b,∴a·b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a·b=6sin2α+5sinαcosα-4cos2α=0.
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=-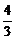 ,或tanα=
,或tanα=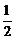 .
.
∵α∈(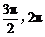 ),tanα<0,故tanα=
),tanα<0,故tanα=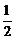 (舍去).∴tanα=-
(舍去).∴tanα=-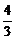 .
.
(2)∵α∈(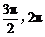 ),∴
),∴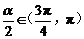 .
.
由tanα=-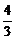 ,求得
,求得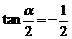 ,
,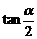 =2(舍去).∴
=2(舍去).∴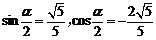 ,
,
cos(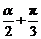 )=
)=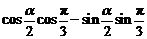 =
=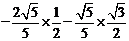 =
=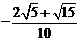 .
.
3.已知: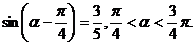 (1)求
(1)求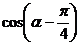 的值;(2)求
的值;(2)求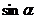 的值;(3)问:函数
的值;(3)问:函数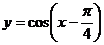 的图像可以通过函数
的图像可以通过函数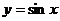 的图像进行怎样的平已得到?
的图像进行怎样的平已得到?
解:(1)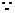
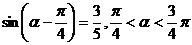 ,
, 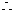
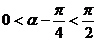
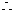
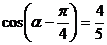
(2)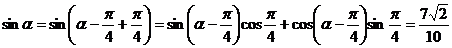 ……..9分
……..9分
(3)函数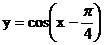 的图像可以通过函数
的图像可以通过函数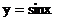 的图像向左平移
的图像向左平移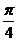 个单位得到
个单位得到
2.设向量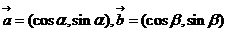 ,
,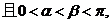
若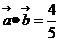 ,
,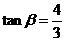 ,求
,求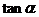 的值。
的值。
解:
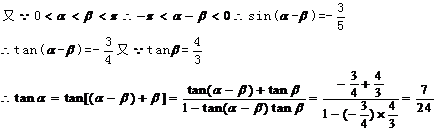
1。已知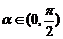 ,
,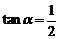 ,求
,求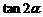 和
和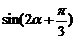 的值.
的值.
解: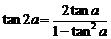
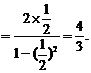

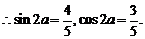
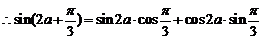
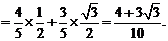
4.某银行准备新设一种存款业务,经预测,存款量与利率的平方成正比,比例系数为k(k>0),贷款的利率为4.8%,又银行吸收的存款能够全部放贷出去。
(1)若存款的利率为x, x∈(0,0.048), 试写出存款量g(x)及银行应支付给储户的利息h(x);
(2)存款利率定为多少时,银行可获得最大收益?
解:(1)由题意,存款量g(x)=Kx2,银行应支付的利息 h(x)=x·g(x)= Kx3 ………… (4分)
(2)设银行可获收益为y,则
y=0.048·Kx2–Kx3 ………………(6分)
y’=K·0.096x–3 Kx2 令y’ =0 即K×0.096x–3 Kx2=0
解得x=0 或x=0.032 …………………(9分)
又当x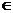 (0,0.032)时,y’>0, x
(0,0.032)时,y’>0, x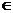 (0.032,0.048)时, y’<0
(0.032,0.048)时, y’<0
 y在(0,0.032)内单调递增,在(0.032,0.048)
单调递减
y在(0,0.032)内单调递增,在(0.032,0.048)
单调递减
故当x=0.032时,y在(0,0.048)内取得极大值,亦即最大值
答:存款利率为3.2%时,银行可获得最大收益 ………………(12分)
赣马高级中学解答题专题训练---三角函数02
命题:王怀学 审核:王翔
3. 佛山某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量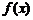 与产量
与产量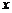 之间的关系式为
之间的关系式为
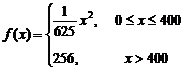 ,每件产品的售价
,每件产品的售价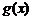 与产量
与产量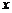 之间的关系式为
之间的关系式为
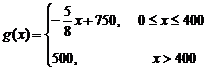 .(Ⅰ)写出该陶瓷厂的日销售利润
.(Ⅰ)写出该陶瓷厂的日销售利润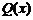 与产量
与产量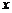 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
解:(Ⅰ)总成本为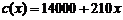 .所以日销售利润
.所以日销售利润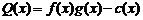
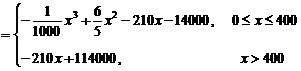 .
……6分
.
……6分
(Ⅱ)①当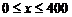 时,
时,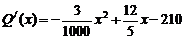 .
……7分
.
……7分
令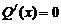 ,解得
,解得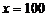 或
或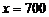 .
……8分
.
……8分
于是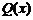 在区间
在区间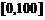 上单调递减,在区间
上单调递减,在区间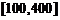 上单调递增,所以
上单调递增,所以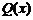 在
在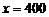 时取到最大值,且最大值为30000;
……10分
时取到最大值,且最大值为30000;
……10分
②当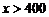 时,
时,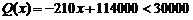 .
……12分
.
……12分
综上所述,若要使得日销售利润最大,每天该生产400件产品,其最大利润为30000元
2.某企业投入81万元经销某产品,经销时间共6个月,市场调研表明,该企业在经销这个产品期间第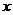 个月的利润
个月的利润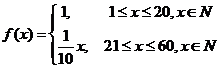 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第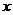 个月的当月利润率
个月的当月利润率
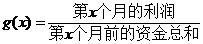 ,例如:
,例如: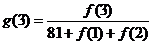
(1)求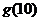 (2)求第
(2)求第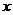 个月的当月利润率
个月的当月利润率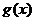
(3)该企业经销此产品期间,哪一个月的当月利润率最大,并求该月的当月利润率
(1)由题意得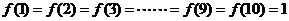
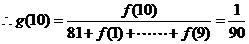
(2)当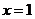 时,
时,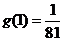 ,当
,当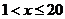 时,
时,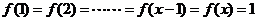
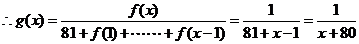
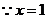 时上式成立。
时上式成立。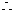 当
当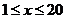 时,
时,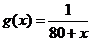 当
当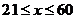 时,
时,
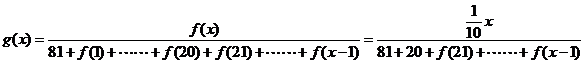
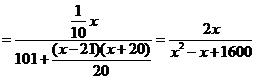
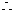 当第
当第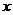 个月的当月利润率
个月的当月利润率
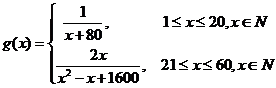 当
当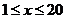 时,
时,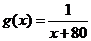 是减函数,此时
是减函数,此时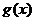 的最大值为
的最大值为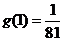 ;当
;当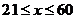 时,
时,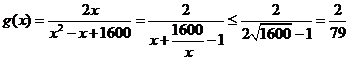
当且仅当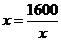 时,即
时,即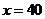 时,
时,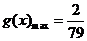 ,又
,又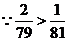 ,
,
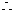 当
当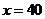 时,
时,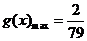 答:该企业经销此产品期间,第40个月的当月利润率最大,最大值为
答:该企业经销此产品期间,第40个月的当月利润率最大,最大值为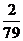
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com