
题目列表(包括答案和解析)
19. (本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知数列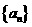 满足
满足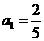 ,且对任意
,且对任意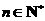 ,都有
,都有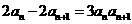 .
.
(1) 求证:数列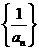 为等差数列;
为等差数列;
(2) 试问数列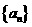 中任意连续两项的乘积
中任意连续两项的乘积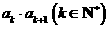 是否仍是
是否仍是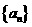 中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.
中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.
18. (本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
在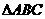 中,角
中,角 、
、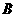 、
、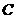 的对边分别为
的对边分别为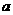 、
、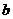 、
、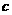 ,且
,且 .
.
(1) 求证: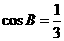 ;
;
(2) 若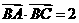 ,且
,且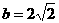 ,求
,求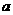 和
和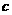 的值.
的值.
17. (本题满分12分)
已知函数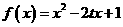 ,
,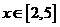 有反函数,且函数
有反函数,且函数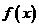 的最大值为
的最大值为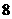 ,求实数
,求实数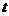 的值.
的值.
16.
已知正方形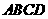 的面积为
的面积为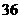 ,
,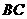 平行于
平行于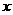 轴,顶点
轴,顶点 、
、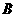 和
和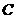 分别在函数
分别在函数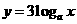 、
、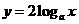 和
和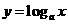 (其中
(其中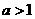 )的图像上,则实数
)的图像上,则实数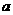 的值为 ( )
的值为 ( )
(A)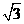 (B)
(B)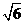 (C)
(C)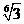 (D)
(D) 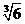
15.
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数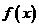 的图像恰好通过
的图像恰好通过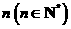 个整点,则称函数
个整点,则称函数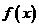 为
为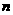 阶整点函数.有下列函数:
阶整点函数.有下列函数:
①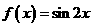 ②
②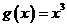 ③
③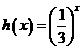 ④
④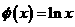 ,
,
其中是一阶整点函数的个数为 ( )
(A)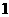 (B)
(B)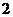 (C)
(C)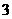 (D)
(D)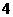
14.
已知无穷等比数列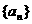 的前
的前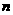 项和为
项和为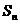 ,各项的和为
,各项的和为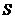 ,且
,且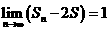 ,则其首项
,则其首项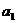 的取值范围是
( )
的取值范围是
( )
(A) (B)
(B)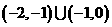
(C) 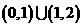 (D)
(D)
13.
圆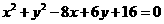 与圆
与圆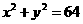 的位置关系是
( )
的位置关系是
( )
(A) 相交 (B) 相离 (C) 内切 (D) 外切
12.
在解决问题:“证明数集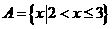 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明.
假设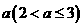 是
是 中的最小数,则取
中的最小数,则取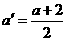 ,可得:
,可得: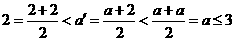 ,与假设中“
,与假设中“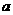 是
是 中的最小数”矛盾!
中的最小数”矛盾!
那么对于问题:“证明数集 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设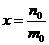 是
是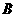 中的最大数,则可以找到
中的最大数,则可以找到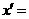 ____________(用
____________(用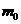 ,
,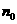 表示),由此可知
表示),由此可知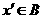 ,
,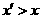 ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集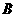 没有最大数.
没有最大数.
11.
已知函数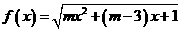 的值域是
的值域是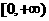 ,则实数
,则实数 的取值范围是________________.
的取值范围是________________.
10. 如图,已知一个多面体的平面展开图由一边长为1的正方体和4个边长为1的正三角形组成,则该多面体的体积是____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com