
题目列表(包括答案和解析)
4. 解(Ⅰ)由已知得,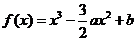 由
由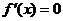 ,得
,得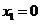 ,
,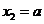 .
.
∵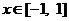 ,
,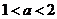 ,∴ 当
,∴ 当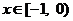 时,
时,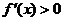 ,
, 递增;
递增;
当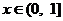 时,
时,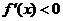 ,
, 递减.
递减.
∴  在区间
在区间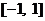 上的最大值为
上的最大值为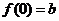 ,∴
,∴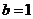 .……………………………2分
.……………………………2分
又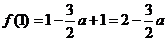 ,
,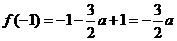 ,∴
,∴ 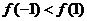 .
.
由题意得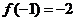 ,即
,即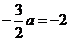 ,得
,得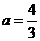 .故
.故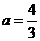 ,
,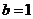 为所求. (Ⅱ)解:由(1)得
为所求. (Ⅱ)解:由(1)得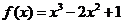 ,
, ,点
,点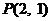 在曲线
在曲线 上.
上.
⑴ 当切点为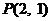 时,切线
时,切线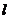 的斜率
的斜率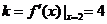 ,
,
∴ 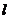 的方程为
的方程为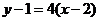 ,即
,即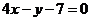 . ………………………………5分
. ………………………………5分
⑵当切点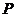 不是切点时,设切点为
不是切点时,设切点为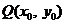
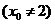 ,切线
,切线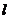 的斜率
的斜率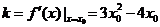 ,∴
,∴ 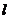 的方程为
的方程为 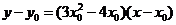 .
.
又点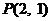 在
在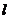 上,∴
上,∴ 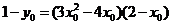 ,
,
∴ 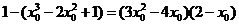 ,∴
,∴ 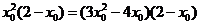 ,
,
∴  ,即
,即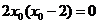 ,∴
,∴ . ∴ 切线
. ∴ 切线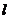 的方程为
的方程为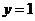 .…8分
.…8分
故所求切线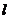 的方程为
的方程为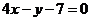 或
或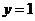 .
………………………………9分
.
………………………………9分
( 或者:由(1)知点A(0,1)为极大值点,所以曲线 的点A处的切线为
的点A处的切线为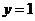 ,恰好经过点
,恰好经过点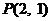 ,符合题意.)
,符合题意.)
赣马高级中学解答题专题训练导数(二)
1解.(I)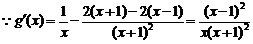 ,
,
当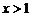 时,
时,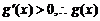 在
在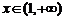 上是单调增函数.
上是单调增函数.
(II) ,
,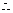 原不等式即为
原不等式即为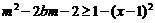 在
在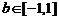 时恒成立.
时恒成立.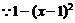 的最大值为1,
的最大值为1, 在
在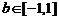 时恒成立.
时恒成立.
令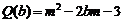 ,则
,则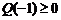 ,且
,且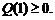 由
由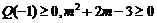 ,解得
,解得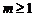 或
或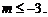 由
由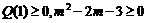 ,解得
,解得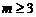 或
或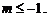
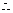 综上得,
综上得,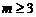 或
或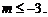
2 解 (1)∵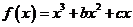 ,∴
,∴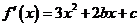 .从而
.从而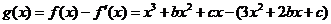 =
=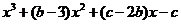
是一个奇函数,所以 得
得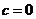 ,由奇函数定义得
,由奇函数定义得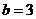 ;
;
(2)由(Ⅰ)知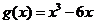 ,从而
,从而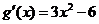 ,由此可知,
,由此可知,
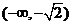 和
和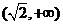 是函数
是函数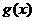 是单调递增区间;
是单调递增区间;
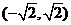 是函数
是函数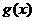 是单调递减区间;
是单调递减区间;
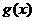 在
在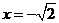 时,取得极大值,
时,取得极大值,
极大值为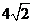 ,
,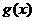 在
在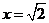 时,取得极小值,极小值为
时,取得极小值,极小值为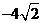 .
.
3(Ⅰ)解: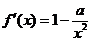 ,由导数的几何意义得
,由导数的几何意义得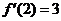 ,于是
,于是 .
.
由切点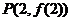 在直线
在直线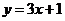 上可得
上可得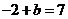 ,解得
,解得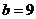 .
.
所以函数 的解析式为
的解析式为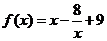 .
.
(Ⅱ)解: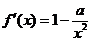 .
.
当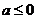 时,显然
时,显然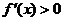 (
(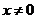 ).这时
).这时 在
在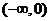 ,
,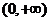 上内是增函数.
上内是增函数.
当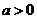 时,令
时,令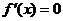 ,解得
,解得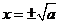 .当
.当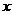 变化时,
变化时,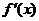 ,
, 的变化情况如下表:
的变化情况如下表:
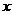 |
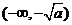 |
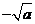 |
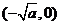 |
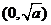 |
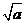 |
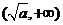 |
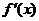 |
+ |
0 |
- |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
↘ |
极小值 |
↗ |
所以 在
在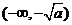 ,
,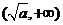 内是增函数,在
内是增函数,在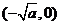 ,
,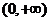 内是减函数.
内是减函数.
(Ⅲ)解:由(Ⅱ)知, 在
在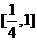 上的最大值为
上的最大值为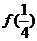 与
与 的较大者,对于任意的
的较大者,对于任意的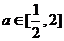 ,不等式
,不等式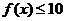 在
在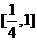 上恒成立,当且仅当
上恒成立,当且仅当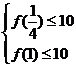 ,即
,即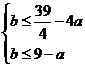 ,对任意的
,对任意的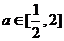 成立.从而得
成立.从而得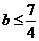 ,所以满足条件的
,所以满足条件的 的取值范围是
的取值范围是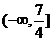 .
.
4解:(Ⅰ)因为函数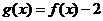 为奇函数,
为奇函数,
所以,对任意的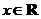 ,
,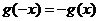 ,即
,即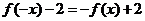 .
.
又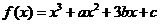 所以
所以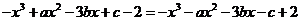 .
.
所以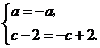 解得
解得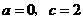 .
.
(Ⅱ)由(Ⅰ)得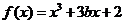 .所以
.所以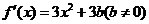 .
.
当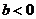 时,由
时,由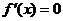 得
得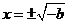 .
.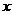 变化时,
变化时,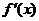 的变化情况如下表:
的变化情况如下表:
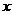 |
 |
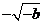 |
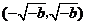 |
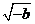 |
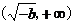 |
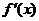 |
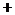 |
0 |
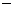 |
0 |
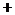 |
所以,当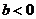 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在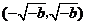 上单调递减,
上单调递减,
在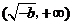 上单调递增.当
上单调递增.当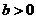 时,
时,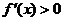 ,所以函数
,所以函数 在
在 上单调递增.
上单调递增.
赣马高级中学解答题专题训练导数(三)
1解:(1)令f(x)=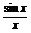 (0<x<π),则f′(x)=
(0<x<π),则f′(x)=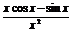 .
.
令g(x)=xcosx-sinx,则g′(x)=-xsinx.所以当0<x<π时,g′(x)=-xsinx<0,
所以g(x)=xcosx-sinx在(0,π)上是递减的,
由连续性知g(x)=xcosx-sinx在[0,π]上也是递减的.
所以当0<x<π时,g(x) <g(0)=0. (6分)
所以f′(x)=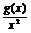 <0,所以f(x)在(0,π)上是递减的.
<0,所以f(x)在(0,π)上是递减的.
而0<α<β<π,所以f(α) >f(β)。
即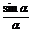 >
>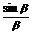 ,故命题成立,
(8分)
,故命题成立,
(8分)
(2)令∠A=α ∠B=2α
∠B=2α ∠C=π-3α,则由正弦定理和诱导公式有
∠C=π-3α,则由正弦定理和诱导公式有
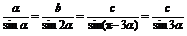 ,即
,即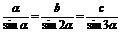 .
(11分)
.
(11分)
而0<α<2α<3α<π,所以由(1)的结论有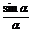 >
>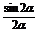 >
>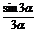 . (12分)
. (12分)
将正弦定理代入即得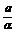 >
>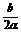 >
>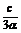

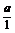 >
>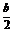 >
>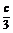 ,即6a>3b>2c
,即6a>3b>2c
2解:(1)方程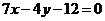 可化为
可化为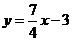 ,当
,当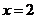 时,
时,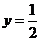 ;
;
又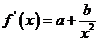 ,于是
,于是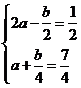 ,解得
,解得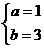 ,故
,故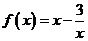
(2)设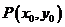 为曲线上任一点,由
为曲线上任一点,由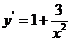 知曲线在点
知曲线在点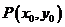 处的切线方程为
处的切线方程为
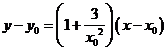 ,即
,即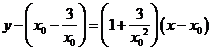
令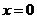 ,得
,得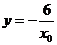 ,从而得切线与直线
,从而得切线与直线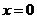 的交点坐标为
的交点坐标为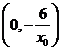 ;
;
令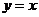 ,得
,得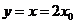 ,从而得切线与直线
,从而得切线与直线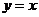 的交点坐标为
的交点坐标为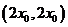 ;
;
所以点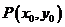 处的切线与直线
处的切线与直线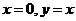 所围成的三角形面积为
所围成的三角形面积为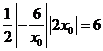 ;
;
故曲线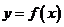 上任一点处的切线与直线
上任一点处的切线与直线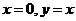 所围成的三角形面积为定值,此定值为6;
所围成的三角形面积为定值,此定值为6;
3[解析]设楼房每平方米的平均综合费为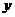 元,依题意得
元,依题意得
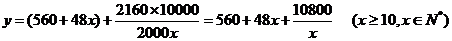
则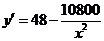 ,令
,令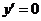 ,即
,即 ,解得
,解得
当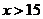 时,
时,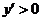 ;当
;当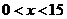 时,
时, ,
,
因此,当 时,
时,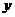 取得最小值,
取得最小值,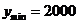 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层。
4 解:设AN的长为x米(x >2)
∵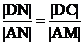 ,∴|AM|=
,∴|AM|=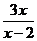
∴SAMPN=|AN|•|AM|=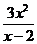 ------------------------------------- 4分
------------------------------------- 4分
(1)由SAMPN > 32 得 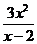 > 32 ,
> 32 ,
∵x >2,∴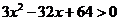 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴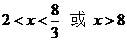 即AN长的取值范围是
即AN长的取值范围是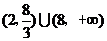 ----------- 8分
----------- 8分
(2)令y=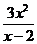 ,则y′=
,则y′=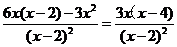 -------------- 10分
-------------- 10分
∵当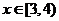 ,y′< 0,∴函数y=
,y′< 0,∴函数y=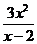 在
在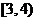 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=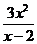 取得最大值,即
取得最大值,即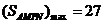 (平方米)
(平方米)
此时|AN|=3米,|AM|=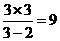 米
---------------------- 12分
米
---------------------- 12分
赣马高级中学解答题专题训练导数(四)
2..解:(Ⅰ)依题意知:直线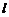 是函数
是函数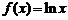 在点
在点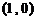 处的切线,故其斜率
处的切线,故其斜率
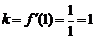 ,所以直线
,所以直线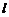 的方程为
的方程为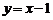 .
.
又因为直线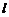 与
与 的图像相切,所以由
的图像相切,所以由
 ,
,
得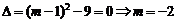 (
(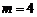 不合题意,舍去);
不合题意,舍去);
3解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=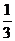 m,
m,
当x变化时,f’(x)与f(x)的变化情况如下表:
|
x |
(-∞,-m) |
-m |
(-m,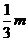 ) ) |
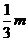 |
(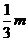 ,+∞) ,+∞) |
|
f’(x) |
 + + |
0 |
- |
0 |
+ |
|
f (x) |
|
极大值 |
|
极小值 |
|
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,
依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-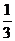 .
.
又f(-1)=6,f(-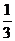 )=
)=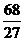 ,所以切线方程为y-6=-5(x+1),或y-
,所以切线方程为y-6=-5(x+1),或y-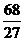 =-5(x+
=-5(x+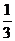 ),
),
即5x+y-1=0,或135x+27y-23=0.
1.解:(I)设切线的斜率为k …………2分
则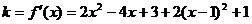 …………4分
…………4分
又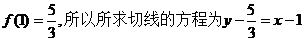
即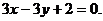 …………6分
…………6分
(II)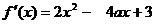
要使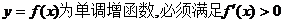
即对任意的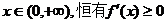 …………8分
…………8分

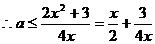 …………10分
…………10分
而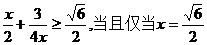 时,等号成立 所以
时,等号成立 所以
所求满足条件的a 值为1
4. 如图, 是沿太湖南北方向道路,
是沿太湖南北方向道路, 为太湖中观光岛屿,
为太湖中观光岛屿,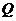 为停车场,
为停车场,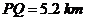 。某旅游团游览完岛屿后,乘游船回停车场
。某旅游团游览完岛屿后,乘游船回停车场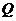 ,已知游船以
,已知游船以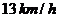 的速度沿方位角
的速度沿方位角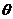 的方向行驶,
的方向行驶,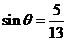 ,游船离开观光岛屿3分钟后,因事耽搁没有来得及登上游船的游客甲为了及时赶到停车地点
,游船离开观光岛屿3分钟后,因事耽搁没有来得及登上游船的游客甲为了及时赶到停车地点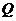 与旅游团会合,决定立即租用小船先到达湖滨大道
与旅游团会合,决定立即租用小船先到达湖滨大道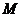 处,然后乘出租汽车到点
处,然后乘出租汽车到点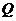 (设游客甲到达湖滨大道后立即乘到出租车)。假设游客甲乘小船行驶的方向是方位角
(设游客甲到达湖滨大道后立即乘到出租车)。假设游客甲乘小船行驶的方向是方位角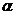 ,出租汽车的速度为
,出租汽车的速度为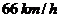 .
.
(Ⅰ)设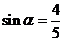 ,问小船的速度为多少
,问小船的速度为多少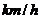 时,游客甲才能和游船同时到达点
时,游客甲才能和游船同时到达点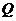 ;
;
 (Ⅱ)设小船速度为
(Ⅱ)设小船速度为 ,请你替游客甲设计小船行驶的方位角
,请你替游客甲设计小船行驶的方位角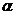 ,当角
,当角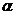 余弦值的大小是多少时,游客甲能按计划以最短时间到达
余弦值的大小是多少时,游客甲能按计划以最短时间到达 .
.
赣马高级中学解答题专题训练导数(一)
3. 已知函数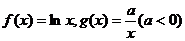 ,设
,设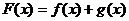 。(Ⅰ)求F(x)的单调区间;
。(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以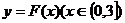 图象上任意一点
图象上任意一点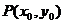 为切点的切线的斜率
为切点的切线的斜率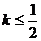 恒成立,求实数
恒成立,求实数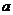 的最小值
的最小值
1.
已知0<α<β<π. (1)求证: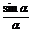 >
>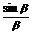 ;(提示:构造函数
;(提示:构造函数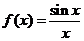 )
)
(2)在△ABC中,已知∠A、∠B、∠C的对边分别为a、b、c,当∠B=2∠A时,判
6a、3b、2c的大小,并说明理由.
2 设函数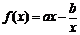 ,曲线
,曲线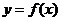 在点
在点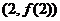 处的切线方程为
处的切线方程为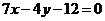 。(1)求
。(1)求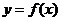 的解析式;
(2)证明:曲线
的解析式;
(2)证明:曲线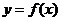 上任一点处的
上任一点处的
切线与直线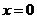 和直线
和直线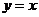 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
3 某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
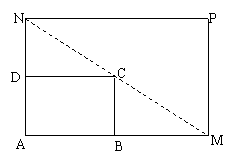
4 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛 AMPN,要求B在AM上,D在AN上,且对角线MN过C点, 已知|AB|=3米,|AD|=2米,
(1) 要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2) 若|AN| 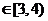 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
赣马高级中学解答题专题训练14
导数(四)编写:刘卫兵 审核:樊继强 王怀学
1 。 已知函数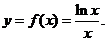 (Ⅰ)求函数
(Ⅰ)求函数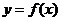 的图象在
的图象在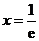 处的切线方程;
处的切线方程;
(Ⅱ)求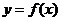 的最大值;
的最大值;
2 已知函数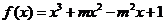 (
(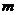 为常数,且
为常数,且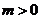 )有极大值9.
)有极大值9.
(Ⅰ)求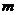 的值;(Ⅱ)若斜率为-5的直线是曲线
的值;(Ⅱ)若斜率为-5的直线是曲线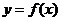 的切线,求此直线方程.
的切线,求此直线方程.
4.已知函数 的导数
的导数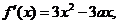
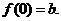
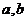 为实数,
为实数,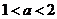 .
.
(Ⅰ)若 在区间
在区间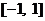 上的最小值、最大值分别为
上的最小值、最大值分别为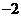 、1,求
、1,求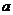 、
、 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求经过点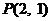 且与曲线
且与曲线 相切的直线
相切的直线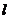 的方程;
的方程;
赣马高级中学解答题专题训练12
导数(二)编写:刘卫兵 审核:樊继强 王怀学
1 设函数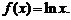 (I)证明函数
(I)证明函数 在
在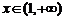 上是单调增函数;
上是单调增函数;
(II)若不等式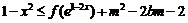 ,当
,当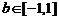 时恒成立,求实数m的取值范围.
时恒成立,求实数m的取值范围.
2 设函数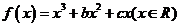 ,已知
,已知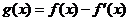 是奇函数.
是奇函数.
(1)求 、
、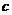 的值.
的值.
(2)求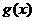 的单调区间与极值.
的单调区间与极值.
3 已知函数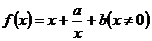 ,其中
,其中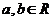 .
.
(Ⅰ)若曲线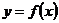 在点
在点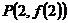 处的切线方程为
处的切线方程为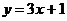 ,求函数
,求函数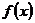 的解析式;
的解析式;
(Ⅱ)讨论函数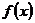 的单调性;
的单调性;
Ⅲ)若对于任意的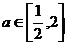 ,不等式
,不等式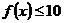 在
在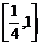 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
4 已知函数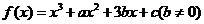 ,且
,且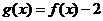 是奇函数.
是奇函数.
(Ⅰ)求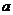 ,
,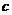 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
赣马高级中学解答题专题训练13
导数(三)编写:刘卫兵 审核:樊继强 王怀学
1.已知函数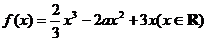 ,
,
(I)若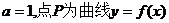 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(II)若函数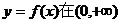 上为单调增函数,试求满足条件的最大整数a的值。
上为单调增函数,试求满足条件的最大整数a的值。
2 已知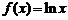 ,
,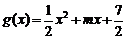 (
( ),直线
),直线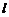 与函数
与函数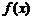 、
、 的图像都相切,且与函数
的图像都相切,且与函数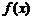 的图像的切点的横坐标为1.求直线
的图像的切点的横坐标为1.求直线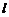 的方程及
的方程及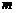 的值;
的值;
3 已知函数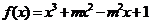 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为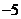 的直线是曲线
的直线是曲线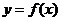 的切线,求此直线方程.
的切线,求此直线方程.
5.某港口水的深度
y(米)是时间t(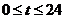 ,单位:时)的函数,记作y=f(t),下面是某日水深的数据:经长期观察,y=f(t)的曲线可以近似地看成函数
,单位:时)的函数,记作y=f(t),下面是某日水深的数据:经长期观察,y=f(t)的曲线可以近似地看成函数 的图象.
的图象.
(Ⅰ)试根据以上数据,求出函数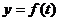 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需的时间).
解:(Ⅰ)由已知数据,易知函数y=f(t)的周期T=12,振幅A=3, b=10,∴ (0≤t≤24)
(0≤t≤24)
(Ⅱ)由题意,该船进出港时,水深应不小于5+6.5=11.5(米) ∴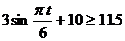 ∴
∴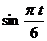
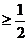 解得,
解得, ;
; 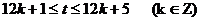 在同一天内,取k=0或1 ∴1≤t≤5或13≤t≤17
在同一天内,取k=0或1 ∴1≤t≤5或13≤t≤17
∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时。
4.已知矩形纸片ABCD中,AB=6 ,AD=12
,AD=12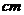 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设

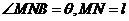 。(Ⅰ)试将
。(Ⅰ)试将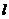 表示成
表示成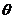 的函数;(Ⅱ)求
的函数;(Ⅱ)求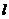 的最小值。
的最小值。
解:(Ⅰ)如图所示,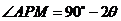 ,则MB=
,则MB=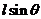 ,
,
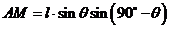 ,由题设得:
,由题设得: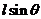 +
+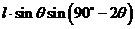 =6,从而得
=6,从而得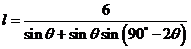 ,即:
,即: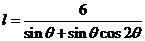 ,
,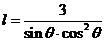
由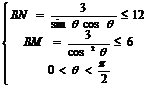 得:
得: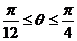 故:
故: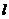 表示成
表示成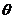 的函数为:
的函数为: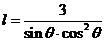 ,(
,(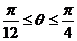 )
)
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
(Ⅱ)设: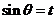 则
则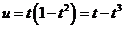 ,即
,即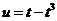 ,
,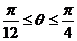 ,
,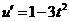 令
令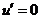 ,得
,得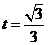 当
当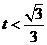 时,
时,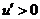 ,当
,当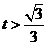 时,
时,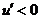 ,所以当
,所以当 时,
时,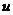 取到最大值:
取到最大值: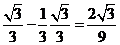 ,
,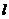 的最小值为
的最小值为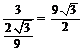
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com