
题目列表(包括答案和解析)
1.正三角形ABC的边长为2,P,Q分别是边AB、AC上的动点,且满足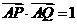 ,设线段AP长为x,线段PQ长为y,
,设线段AP长为x,线段PQ长为y,
(1)试求y随x变化而变化的函数关系式y=f(x);
(2)试求函数y=f(x)的值域。
(1) (2)
(2)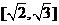
5.解:(1)由A(0,1)满足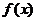 解析式
解析式 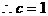 ,又
,又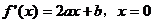 时
时
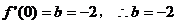
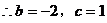 ………………4分
………………4分
(2)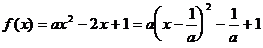
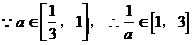
∴当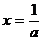 时,
时,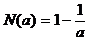 ………………6分
………………6分
当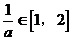 时,
时,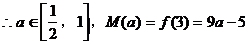 ………………8分
………………8分
当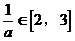 时,
时,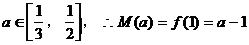 ………………10分
………………10分
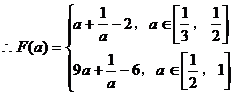 ……………………12分
……………………12分
赣马高级中学解答题专题训练01函数(二)答案
命题:王怀学 审核:王翔
4.已知函数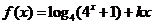
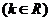 是偶函数.
是偶函数.
设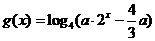 ,若函数
,若函数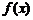 与
与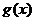 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数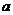 的取值范围.
的取值范围.
解: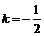 ;
;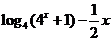
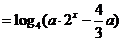 有一个解,
有一个解, 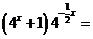
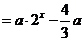
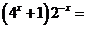
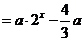 ,
,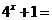
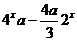 ,
,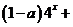
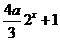 =0,令
=0,令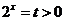 则
则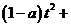
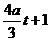 =0 方程有正数解,令
=0 方程有正数解,令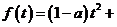
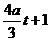 图象过/0,1/点,开口向上时,与轴切于正半轴,
图象过/0,1/点,开口向上时,与轴切于正半轴,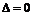 ;开口向下,一定相交与正半轴。。。。。。。。总之,得到
;开口向下,一定相交与正半轴。。。。。。。。总之,得到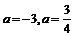 或
或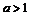
3.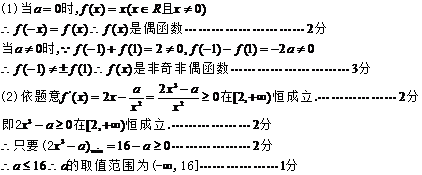
2.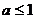 ;
; 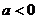 时
时 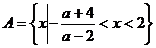
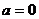 时
时 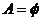
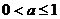 时
时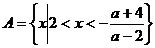
1。解 (1)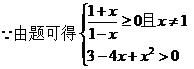
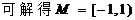 (…………4分)
(…………4分)
(2)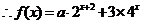 =
=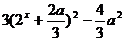
又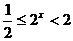 ,
,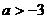 ,
,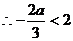 (…………………6分)
(…………………6分)
①若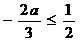 ,即
,即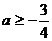 时,
时,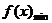 =
=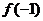 =
=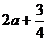 ,(…………8分)
,(…………8分)
②若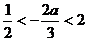 ,即
,即
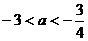 时,
时,
所以当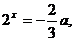 即
即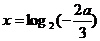 时,
时,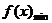 =
=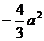 (………………11分)
(………………11分)
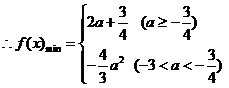
5.某港口水的深度
y(米)是时间t(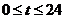 ,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
经长期观察,y=f(t)的曲线可以近似地看成函数 的图象.
的图象.
(Ⅰ)试根据以上数据,求出函数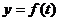 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需的时间).
赣马高级中学解答题专题训练01答案
函数(一)
4. 已知矩形纸片ABCD中,AB=6
已知矩形纸片ABCD中,AB=6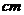 ,AD=12
,AD=12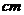 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设
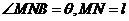 。
。
(Ⅰ)试将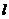 表示成
表示成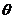 的函数;
的函数;
(Ⅱ)求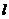 的最小值。
的最小值。
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
3。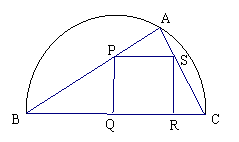 如图,某小区准备绿化一块直径为
如图,某小区准备绿化一块直径为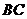 的半圆形空地,
的半圆形空地,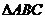 外的地方种草,
外的地方种草,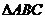 的内接正方形
的内接正方形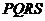 为一水池,其余地方种花.若
为一水池,其余地方种花.若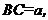
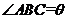 ,设
,设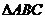 的面积为
的面积为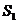 ,正方形
,正方形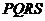 的面积为
的面积为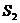 ,将比值
,将比值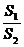 称为“规划合理度”.
称为“规划合理度”.
(1)①试用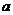 ,
,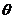 表示
表示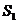 ; ②. 试用
; ②. 试用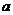 ,
,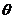 表示
表示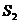
(2)当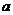 为定值,
为定值,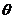 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角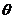 的大小.
的大小.
2.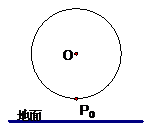 如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为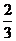 m,圆环的圆心距离地面的高度为1m,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
m,圆环的圆心距离地面的高度为1m,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度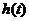 ;
;
(2)画出函数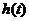 在
在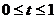 时的图象;
时的图象;
(3)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过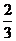 m?
m?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com